1.1 Вероятностное пространство

σ σ sigma\sigmaσ-алгебра. Измеримое пространство. Примеры борелевских подмножеств. Вероятностное пространство. Примеры вероятностных пространств
Пусть Ω Ω Omega\OmegaΩ - множество элементов, которые называются элементарными исходами или элементарными событиями. Непустой класс A A A\mathcal{A}A подмножеств из Ω Ω Omega\OmegaΩ, замкнутый относительно операции дополнения и операций объединения конечного и счетного числа своих подмножеств, называется σ σ sigma\sigmaσ-алгеброй на Ω Ω Omega\OmegaΩ, а сами подмножества - событиями. Приведенные ниже два тождества
( ⋂ j ∈ I A j ) C = ⋃ j ∈ I A j C и ( ⋃ j ∈ I A j ) C = ⋂ j ∈ I A j C , ⋂ j ∈ I   A j C = ⋃ j ∈ I   A j C  и  ⋃ j ∈ I   A j C = ⋂ j ∈ I   A j C , (nnn_(j in I)A_(j))^(C)=uuu_(j in I)A_(j)^(C)" и "(uuu_(j in I)A_(j))^(C)=nnn_(j in I)A_(j)^(C),\left(\bigcap_{j \in I} A_{j}\right)^{C}=\bigcup_{j \in I} A_{j}^{C} \text { и }\left(\bigcup_{j \in I} A_{j}\right)^{C}=\bigcap_{j \in I} A_{j}^{C},(⋂j∈IAj)C=⋃j∈IAjC и (⋃j∈IAj)C=⋂j∈IAjC,
в которых буква I I III обозначает произвольное множество индексов, называются формулами двойственности. Используя первое тождество, можно показать, что σ σ sigma\sigmaσ-алгебра замкнута также относительно конечных и счетных пересечений. Если A A AAA - событие, то его дополнение A C A C A^(C)A^{C}AC также является событием. Поэтому все множество Ω = A ∪ A C Ω = A ∪ A C Omega=A uuA^(C)\Omega=A \cup A^{C}Ω=A∪AC, а также пустое подмножество ∅ = A ∩ A C ∅ = A ∩ A C O/=A nnA^(C)\emptyset=A \cap A^{C}∅=A∩AC также являются событиями. Они называются достоверным и невозможным событиями соответственно. Легко убедиться непосредственной проверкой, что
минимальная σ σ sigma\sigmaσ-алгебра, содержащая событие A A AAA, состоит из четырех подмножеств { ∅ , A , A C , Ω } ∅ , A , A C , Ω {O/,A,A^(C),Omega}\left\{\varnothing, A, A^{C}, \Omega\right\}{∅,A,AC,Ω}. В качестве другого очевидного примера σ σ sigma\sigmaσ-алгебры можно указать множество всех подмножеств Ω Ω Omega\OmegaΩ. Обычно именно такие σ σ sigma\sigmaσ-алгебры используются в тех случаях, когда множество Ω Ω Omega\OmegaΩ является конечным или счетным. Пару, состоящую из множества Ω Ω Omega\OmegaΩ элементарных исходов и σ σ sigma\sigmaσ-алгебры A A A\mathcal{A}A его подмножеств, принято называть измеримым пространством ( Ω , A ) ( Ω , A ) (Omega,A)(\Omega, \mathcal{A})(Ω,A).
Пусть K K KKK - произвольное множество индексов, ( B k ) k ∈ K B k k ∈ K (B_(k))_(k in K)\left(B_{k}\right)_{k \in K}(Bk)k∈K - непустое семейство подмножеств из Ω Ω Omega\OmegaΩ, а A ( B k , k ∈ K ) A B k , k ∈ K A(B_(k),k in K)\mathcal{A}\left(B_{k}, k \in K\right)A(Bk,k∈K) - пересечение всех σ σ sigma\sigmaσ-алгебр, содержащих это семейство. Одной из таких σ σ sigma\sigmaσ-алгебр является σ σ sigma\sigmaσ-алгебра всех подмножеств Ω Ω Omega\OmegaΩ. Очевидно, что ( B k ) k ∈ K B k k ∈ K (B_(k))_(k in K)\left(B_{k}\right)_{k \in K}(Bk)k∈K принадлежит этому пересечению, которое также является σ σ sigma\sigmaσ-алгеброй. Эта σ σ sigma\sigmaσ-алгебра называется σ σ sigma\sigmaσ-алгеброй, порожденной семейством ( B k ) k ∈ K B k k ∈ K (B_(k))_(k in K)\left(B_{k}\right)_{k \in K}(Bk)k∈K, и является наименьшей σ σ sigma\sigmaσ-алгеброй, содержащей это семейство. В частности, приведенная выше σ σ sigma\sigmaσ-алгебра { ∅ , A , A C , Ω } ∅ , A , A C , Ω {O/,A,A^(C),Omega}\left\{\varnothing, A, A^{C}, \Omega\right\}{∅,A,AC,Ω} является наименьшей σ σ sigma\sigmaσ-алгеброй A ( A ) A ( A ) A(A)\mathcal{A}(A)A(A), порожденной подмножеством A ∈ Ω A ∈ Ω A in OmegaA \in \OmegaA∈Ω.
Пример σ σ sigma\sigmaσ-алгебры ...
Далее будет часто использоваться σ σ sigma\sigmaσ-алгебра, порожденная всеми интервалами вещественной прямой R R RRR. Она называется борелевской σ σ sigma\sigmaσ-алгеброй и обозначается символом B . σ B . σ B.sigma\mathcal{B} . \sigmaB.σ-Алгебра, порожденная v v vvv-мерными интервалами из R v R v R^(v)R^{\boldsymbol{v}}Rv, которые называются также гиперинтервалами или гиперпараллелепипедами, также называется борелевской и обозначается символом B v B v B^(v)\mathcal{B}^{v}Bv. Ниже приводятся примеры подмножеств σ σ sigma\sigmaσ-алгебры B B B\mathcal{B}B, которые называются борелевскими множествами на прямой R R RRR.
(1.1.1) Каждая точка a a aaa прямой R R RRR является борелевским подмножеством, состоящим из одного элемента. Это следует из того, что любая точка a ∈ R a ∈ R a in Ra \in Ra∈R есть счетное пересечение открытых интервалов
{ a } = ⋂ n > 1 ] a + 1 n , a − 1 n [ { a } = ⋂ n > 1   a + 1 n , a − 1 n [ {:{a}=nnn_(n > 1)]a+(1)/(n),a-(1)/(n)[\left.\{a\}=\bigcap_{n>1}\right] a+\frac{1}{n}, a-\frac{1}{n}[{a}=⋂n>1]a+1n,a−1n[
открытых интервалов, которые являются борелевскими подмножествами.
(1.1.2) Множество Q Q QQQ точек с рациональными координатами является борелевским, так как оно есть объединение счетного числа таких точек.
(1.1.3) Множество иррациональных точек является борелевским, так как оно есть дополнение Q c = R ∖ Q Q c = R ∖ Q Q^(c)=R\\QQ^{c}=R \backslash QQc=R∖Q множества рациональных чисел.
(1.1.4) Любое открытое множество на R R RRR является борелевским, так как оно есть объединение конечного или счетного числа попарно пересекающихся своих открытых интервалов.
(1.1.5) Замкнутое множество является борелевским, так как оно есть дополнение открытого множества.
(1.1.6) Если отображение f : [ 0 , 1 ] → R f : [ 0 , 1 ] → R f:[0,1]rarr Rf:[0,1] \rightarrow Rf:[0,1]→R - непрерывно, то при любом c ∈ R c ∈ R c in Rc \in Rc∈R множество { x ∈ [ 0 , 1 ] : f ( x ) ≤ c } { x ∈ [ 0 , 1 ] : f ( x ) ≤ c } {x in[0,1]:f(x) <= c}\{x \in[0,1]: f(x) \leq c\}{x∈[0,1]:f(x)≤c} является замкнутым, а значит борелевским.
Вероятностью на σ σ sigma\sigmaσ-алгебре A A A\mathcal{A}A называется отображение P : A → R P : A → R P:Ararr RP: \mathcal{A} \rightarrow RP:A→R, удовлетворяющее трем аксиомам. Во-первых, отображение P P PPP является неотрицательным: P ( A ) ≥ 0 P ( A ) ≥ 0 P(A) >= 0P(A) \geq 0P(A)≥0 для любого A ∈ A A ∈ A A inAA \in \mathcal{A}A∈A. Во-вторых, отображение P P PPP является нормированным: P ( Ω ) = 1 P ( Ω ) = 1 P(Omega)=1P(\Omega)=1P(Ω)=1. Наконец, отображение P P PPP является счетно-аддитивным отображением. Последнее свойство означает, что для любого конечного или счетного семейства ( A k ) k ∈ K A k k ∈ K (A_(k))_(k in K)\left(A_{k}\right)_{k \in K}(Ak)k∈K попарно непересекающихся подмножеств из A A A\mathcal{A}A имеет место равенство
P ( ∑ k ∈ K A k ) = ∑ k ∈ K P ( A k ) . P ∑ k ∈ K   A k = ∑ k ∈ K   P A k . P(sum_(k in K)A_(k))=sum_(k in K)P(A_(k)).P\left(\sum_{k \in K} A_{k}\right)=\sum_{k \in K} P\left(A_{k}\right) .P(∑k∈KAk)=∑k∈KP(Ak).
Совокупность, состоящая из множества элементарных исходов Ω , σ Ω , σ Omega,sigma\Omega, \sigmaΩ,σ-алгебры событий A A A\mathcal{A}A и вероятности P P PPP на A A A\mathcal{A}A, называется вероятностным пространством и обозначается ( Ω , A , P Ω , A , P Omega,A,P\Omega, \mathcal{A}, PΩ,A,P ).
(1.1.7) Вероятностное пространство с конечным множеством элементарных исходов. Далее для обозначения количества элементов конечного множества Ω Ω Omega\OmegaΩ будет использоваться символ | Ω | | Ω | |Omega||\Omega||Ω|. Если | Ω | < + ∞ | Ω | < + ∞ |Omega| < +oo|\Omega|<+\infty|Ω|<+∞, то в качестве σ σ sigma\sigmaσ-алгебры A A A\mathcal{A}A обычно используют множество всех подмножеств Ω Ω Omega\OmegaΩ. Всегда можно поставить в соответствие каждому элементарному исходу ω ∈ Ω ω ∈ Ω omega in Omega\omega \in \Omegaω∈Ω неотрицательное число P ( { ω } ) ≥ 0 P ( { ω } ) ≥ 0 P({omega}) >= 0P(\{\omega\}) \geq 0P({ω})≥0 такое, что
∑ ω ∈ Ω P ( { ω } ) = 1 ∑ ω ∈ Ω   P ( { ω } ) = 1 sum_(omega in Omega)P({omega})=1\sum_{\omega \in \Omega} P(\{\omega\})=1∑ω∈ΩP({ω})=1
В самом деле, пусть n = | Ω | n = | Ω | n=|Omega|n=|\Omega|n=|Ω|. Перенумеруем элементы Ω Ω Omega\OmegaΩ, выберем в интервале ] 0 , 1 [ ] 0 , 1 ]0,1[:}] 0,1\left[\right.]0,1[ точки ( x j ) 1 ≤ j ≤ n − 1 x j 1 ≤ j ≤ n − 1 (x_(j))_(1 <= j <= n-1)\left(x_{j}\right)_{1 \leq j \leq n-1}(xj)1≤j≤n−1 таким образом, чтобы x 1 ≤ x 2 ≤ ⋯ ≤ x n − 1 x 1 ≤ x 2 ≤ ⋯ ≤ x n − 1 x_(1) <= x_(2) <= cdots <= x_(n-1)x_{1} \leq x_{2} \leq \cdots \leq x_{n-1}x1≤x2≤⋯≤xn−1 и определим n n nnn чисел ( p j ) 1 ≤ j ≤ n p j 1 ≤ j ≤ n (p_(j))_(1 <= j <= n)\left(p_{j}\right)_{1 \leq j \leq n}(pj)1≤j≤n следующим образом
p 1 = x 1 p j = x j − x j − 1 , 2 ≤ j ≤ n − 1 p n = 1 − p n − 1 p 1 = x 1 p j = x j − x j − 1 , 2 ≤ j ≤ n − 1 p n = 1 − p n − 1 {:[p_(1)=x_(1)],[p_(j)=x_(j)-x_(j-1)","2 <= j <= n-1],[p_(n)=1-p_(n-1)]:}\begin{aligned} & p_{1}=x_{1} \\ & p_{j}=x_{j}-x_{j-1}, 2 \leq j \leq n-1 \\ & p_{n}=1-p_{n-1} \end{aligned}p1=x1pj=xj−xj−1,2≤j≤n−1pn=1−pn−1
Нетрудно убедиться в том, что p 1 + , , , + p n = 1 p 1 + , , , + p n = 1 p_(1)+,,,+p_(n)=1p_{1}+,,,+p_{n}=1p1+,,,+pn=1.
Для любого подмножества B ⊂ Ω B ⊂ Ω B sub OmegaB \subset \OmegaB⊂Ω, которое по определению является событием из A A A\mathcal{A}A, определим число P ( B ) P ( B ) P(B)P(B)P(B) равенством
P ( B ) = ∑ ω ∈ B P ( { ω } ) . P ( B ) = ∑ ω ∈ B   P ( { ω } ) . P(B)=sum_(omega in B)P({omega}).P(B)=\sum_{\omega \in B} P(\{\omega\}) .P(B)=∑ω∈BP({ω}).
Легко показать, что для так определенного отображения P : A → R P : A → R P:Ararr RP: \mathcal{A} \rightarrow RP:A→R выполняются все аксиомы, то есть P P PPP является вероятностью на A A A\mathcal{A}A.
Пусть P P PPP - вероятность на A A A\mathcal{A}A и D ∈ A D ∈ A D inAD \in \mathcal{A}D∈A. Легко убедиться в том, что семейство A D A D A_(D)\mathcal{A}_{D}AD, состоящее из всех пересечений вида A ∩ D A ∩ D A nn DA \cap DA∩D, гле A ∈ A A ∈ A A inAA \in \mathcal{A}A∈A, будет σ σ sigma\sigmaσ-алгеброй подмножеств из D D DDD. При P ( D ) > 0 P ( D ) > 0 P(D) > 0P(D)>0P(D)>0 отображение P D : A D → R P D : A D → R P_(D):A_(D)rarr RP_{D}: \mathcal{A}_{D} \rightarrow RPD:AD→R, определяемое для любого A ∩ D ∈ A D A ∩ D ∈ A D A nn D inA_(D)A \cap D \in \mathcal{A}_{D}A∩D∈AD равенством
P D ( A ∩ D ) = P ( A ∩ D ) P ( D ) , P D ( A ∩ D ) = P ( A ∩ D ) P ( D ) , P_(D)(A nn D)=(P(A nn D))/(P(D)),P_{D}(A \cap D)=\frac{P(A \cap D)}{P(D)},PD(A∩D)=P(A∩D)P(D),
будет вероятностью на A D A D A_(D)\mathcal{A}_{D}AD. Таким образом, совокупность ( D , A D , P D D , A D , P D D,A_(D),P_(D)D, \mathcal{A}_{D}, P_{D}D,AD,PD ) является вероятностным пространством. При этом каждое событие A ∩ D A ∩ D A nn DA \cap DA∩D из A D A D A_(D)\mathcal{A}_{D}AD является событием в A A A\mathcal{A}A. Поэтому вероятностное пространство ( D , A D , P D D , A D , P D D,A_(D),P_(D)D, \mathcal{A}_{D}, P_{D}D,AD,PD ) называется подпространством пространства ( Ω , A , P Ω , A , P Omega,A,P\Omega, \mathcal{A}, PΩ,A,P ).
Так как каждое подмножество B = A ∩ D B = A ∩ D B=A nn DB=A \cap DB=A∩D из A D A D A_(D)\mathcal{A}_{D}AD является подмножеством σ σ sigma\sigmaσ-алгебры A A A\mathcal{A}A и одновременно B ⊂ D B ⊂ D B sub DB \subset DB⊂D, то вероятность P D ( B ) P D ( B ) P_(D)(B)P_{D}(B)PD(B) можно записать следующим образом:
P D ( B ) = P ( B ) P ( D ) = P ( A ∩ D ) P ( D ) = P ( A ∣ D ) . P D ( B ) = P ( B ) P ( D ) = P ( A ∩ D ) P ( D ) = P ( A ∣ D ) . P_(D)(B)=(P(B))/(P(D))=(P(A nn D))/(P(D))=P(A∣D).P_{D}(B)=\frac{P(B)}{P(D)}=\frac{P(A \cap D)}{P(D)}=P(A \mid D) .PD(B)=P(B)P(D)=P(A∩D)P(D)=P(A∣D).

Задачи

  1. Пусть X X XXX - непустое множество, ( A j ) j ∈ J A j j ∈ J (A_(j))_(j in J)\left(A_{j}\right)_{j \in J}(Aj)j∈J - произвольное семейство его подмножеств. Непосредственной проверкой убедиться в справедливости тождеств
( ⋃ j ∈ J A j ) C = ⋂ j ∈ J A j C и ( ⋂ j ∈ J A j ) C = ⋃ j ∈ J A j C , ⋃ j ∈ J   A j C = ⋂ j ∈ J   A j C  и  ⋂ j ∈ J   A j C = ⋃ j ∈ J   A j C , (uuu_(j in J)A_(j))^(C)=nnn_(j in J)A_(j)^(C)" и "(nnn_(j in J)A_(j))^(C)=uuu_(j in J)A_(j)^(C),\left(\bigcup_{j \in J} A_{j}\right)^{C}=\bigcap_{j \in J} A_{j}^{C} \text { и }\left(\bigcap_{j \in J} A_{j}\right)^{C}=\bigcup_{j \in J} A_{j}^{C},(⋃j∈JAj)C=⋂j∈JAjC и (⋂j∈JAj)C=⋃j∈JAjC,
известных под именем формул двойственности.
2. Пусть X X XXX и Y Y YYY - непустые множества, f f fff - отображение вида X → Y X → Y X rarr YX \rightarrow YX→Y, а Θ Θ Theta\ThetaΘ - множество, элементы которого называются индексами. Показать, что при любом B ⊂ Y B ⊂ Y B sub YB \subset YB⊂Y и B θ ⊂ Y , θ ∈ Θ B θ ⊂ Y , θ ∈ Θ B_(theta)sub Y,theta in ThetaB_{\theta} \subset Y, \theta \in \ThetaBθ⊂Y,θ∈Θ, справедливы тождества
f − 1 ( B C ) = ( f − 1 ( B ) ) C , f − 1 ( ⋃ θ ∈ Θ B θ ) = ⋃ θ ∈ Θ f − 1 ( B θ ) f − 1 ( ⋂ θ ∈ Θ B θ ) = ⋂ θ ∈ Θ f − 1 ( B θ ) f − 1 B C = f − 1 ( B ) C , f − 1 ⋃ θ ∈ Θ   B θ = ⋃ θ ∈ Θ   f − 1 B θ f − 1 ⋂ θ ∈ Θ   B θ = ⋂ θ ∈ Θ   f − 1 B θ {:[f^(-1)(B^(C))=(f^(-1)(B))^(C)","quadf^(-1)(uuu_(theta in Theta)B_(theta))=uuu_(theta in Theta)f^(-1)(B_(theta))],[f^(-1)(nnn_(theta in Theta)B_(theta))=nnn_(theta in Theta)f^(-1)(B_(theta))]:}\begin{gathered} f^{-1}\left(B^{C}\right)=\left(f^{-1}(B)\right)^{C}, \quad f^{-1}\left(\bigcup_{\theta \in \Theta} B_{\theta}\right)=\bigcup_{\theta \in \Theta} f^{-1}\left(B_{\theta}\right) \\ f^{-1}\left(\bigcap_{\theta \in \Theta} B_{\theta}\right)=\bigcap_{\theta \in \Theta} f^{-1}\left(B_{\theta}\right) \end{gathered}f−1(BC)=(f−1(B))C,f−1(⋃θ∈ΘBθ)=⋃θ∈Θf−1(Bθ)f−1(⋂θ∈ΘBθ)=⋂θ∈Θf−1(Bθ)
  1. Доказать, что σ σ sigma\sigmaσ-алгебра, порожденная интервалами вида ] − ∞ , x ] , x ∈ R ] − ∞ , x ] , x ∈ R ]-oo,x],x in R]-\infty, x], x \in R]−∞,x],x∈R, вещественной прямой R R RRR, является борелевской.
  2. Привести пример вероятностного пространства с конечным множеством Ω Ω Omega\OmegaΩ элементарных событий.
  3. Привести пример вероятностного пространства со счетным множеством Ω Ω Omega\OmegaΩ элементарных событий.
  4. Привести пример вероятностного пространства с множеством элементарных событий Ω = [ 0 ; 1 ] × [ 0 ; 1 ] Ω = [ 0 ; 1 ] × [ 0 ; 1 ] Omega=[0;1]xx[0;1]\Omega=[0 ; 1] \times[0 ; 1]Ω=[0;1]×[0;1].

1.2 Случайные величины и их распределения

Операция взятия прообраза и ее свойства. Скалярные и векторные случайные величины. Примеры случайных величин. Свойства распределения векторных случайных величин. Дискретные случайные величины. Плотность распределения. Примеры. Числовые характеристики случайных величин.
Пусть ( Ω , A ) ( Ω , A ) (Omega,A)(\Omega, \mathcal{A})(Ω,A) - измеримом пространство, B B B\mathcal{B}B - борелевская σ σ sigma\sigmaσ - алгебра на R R RRR. Отображение вида ξ : Ω → R ξ : Ω → R xi:Omega rarr R\xi: \Omega \rightarrow Rξ:Ω→R называется скалярной случайной величиной, определенной на ( Ω , A Ω , A Omega,A\Omega, \mathcal{A}Ω,A ), если для любого борелевского множества B ∈ B B ∈ B B inBB \in \mathcal{B}B∈B его прообраз
ξ − 1 ( B ) = { ω ∈ Ω : ξ ( ω ) ∈ B ) } ξ − 1 ( B ) = { ω ∈ Ω : ξ ( ω ) ∈ B ) {:xi^(-1)(B)={omega in Omega:xi(omega)in B)}\left.\xi^{-1}(B)=\{\omega \in \Omega: \xi(\omega) \in B)\right\}ξ−1(B)={ω∈Ω:ξ(ω)∈B)}
является событием из A A A\mathcal{A}A.
(1.2.1) Множество C C C\mathcal{C}C всех подмножеств B B BBB из R R RRR, прообразы ξ − 1 ( B ) ξ − 1 ( B ) xi^(-1)(B)\xi^{-1}(B)ξ−1(B) которых являются событиями, есть σ σ sigma\sigmaσ-алгебра.
Доказательство. В соответствии с определением σ σ sigma\sigmaσ-алгебры требуется показать, во-первых, что для любого B ∈ C B ∈ C B inCB \in \mathcal{C}B∈C его дополнение B C ∈ C B C ∈ C B^(C)inCB^{C} \in \mathcal{C}BC∈C. Это утверждение следует из тождества
ξ − 1 ( B C ) = ( ξ − 1 ( B ) ) C ξ − 1 B C = ξ − 1 ( B ) C xi^(-1)(B^(C))=(xi^(-1)(B))^(C)\xi^{-1}\left(B^{C}\right)=\left(\xi^{-1}(B)\right)^{C}ξ−1(BC)=(ξ−1(B))C
В самом деле, пусть B ∈ C B ∈ C B inCB \in \mathcal{C}B∈C. Тогда ξ − 1 ( B ) ξ − 1 ( B ) xi^(-1)(B)\xi^{-1}(B)ξ−1(B) принадлежит σ σ sigma\sigmaσ - алгебре A A A\mathcal{A}A, которая содержит также и его дополнением ( ξ − 1 ( B ) ) C ξ − 1 ( B ) C (xi^(-1)(B))^(C)\left(\xi^{-1}(B)\right)^{C}(ξ−1(B))C. Следовательно, B C B C B^(C)B^{C}BC также принадлежит C C C\mathcal{C}C. Во-вторых, требуется показать, что для любого конечное или счетного семейства ( B j ) j ≥ 1 B j j ≥ 1 (B_(j))_(j >= 1)\left(B_{j}\right)_{j \geq 1}(Bj)j≥1 подмножеств из C C C\mathcal{C}C их объединение также принадлежит C C C\mathcal{C}C. Это следует из тождества
ξ − 1 ( ⋃ j ≥ 1 B j ) = ⋃ j ≥ 1 ξ − 1 ( B j ) ξ − 1 ⋃ j ≥ 1   B j = ⋃ j ≥ 1   ξ − 1 B j xi^(-1)(uuu_(j >= 1)B_(j))=uuu_(j >= 1)xi^(-1)(B_(j))\xi^{-1}\left(\bigcup_{j \geq 1} B_{j}\right)=\bigcup_{j \geq 1} \xi^{-1}\left(B_{j}\right)ξ−1(⋃j≥1Bj)=⋃j≥1ξ−1(Bj)
Что и требовалось доказать.
По определению случайной величины прообраз любого интервала является событием из A A A\mathcal{A}A. Поэтому σ σ sigma\sigmaσ-алгебра C C C\mathcal{C}C содержит все интервалы из R R RRR, а также содержит σ σ sigma\sigmaσ-алгебру B B B\mathcal{B}B, порожденную интервалами (борелевскую).
Пусть v v vvv - натуральное число, ξ = ( ξ j ) 1 ≤ j ≤ v ξ = ξ j 1 ≤ j ≤ v xi=(xi_(j))_(1 <= j <= v)\xi=\left(\xi_{j}\right)_{1 \leq j \leq v}ξ=(ξj)1≤j≤v - семейство отображений вида ξ j : Ω → R ξ j : Ω → R xi_(j):Omega rarr R\xi_{j}: \Omega \rightarrow Rξj:Ω→R. Отображение ξ : Ω → R v ξ : Ω → R v xi:Omega rarrR^(v)\xi: \Omega \rightarrow R^{v}ξ:Ω→Rv, определяемое равенством
ξ ( ω ) = ( ξ 1 ( ω ) , … , ξ v ( ω ) ) , ξ ( ω ) = ξ 1 ( ω ) , … , ξ v ( ω ) , xi(omega)=(xi_(1)(omega),dots,xi_(v)(omega)),\xi(\omega)=\left(\xi_{1}(\omega), \ldots, \xi_{v}(\omega)\right),ξ(ω)=(ξ1(ω),…,ξv(ω)),
называется v v vvv-мерной (или векторной) случайной величиной, определенным на измеримом пространстве ( Ω , A Ω , A Omega,A\Omega, \mathcal{A}Ω,A ), если для любого борелевского множества B ∈ B v B ∈ B v B inB^(v)B \in \mathcal{B}^{v}B∈Bv его прообраз
ξ − 1 ( B ) = { ω ∈ Ω : ξ ( ω ) ∈ B } ξ − 1 ( B ) = { ω ∈ Ω : ξ ( ω ) ∈ B } xi^(-1)(B)={omega in Omega:xi(omega)in B}\xi^{-1}(B)=\{\omega \in \Omega: \xi(\omega) \in B\}ξ−1(B)={ω∈Ω:ξ(ω)∈B}
является событием из A A A\mathcal{A}A.
Ниже перечисляются свойства случайных величин, которые будут использоваться далее. Их доказательства приводятся в курсах по теории вероятностей.
(1.2.2) Пусть ( A k ) k ≥ 1 A k k ≥ 1 (A_(k))_(k >= 1)\left(A_{k}\right)_{k \geq 1}(Ak)k≥1 - счетное семейство попарно непересекающихся событий σ σ sigma\sigmaσ-алгебры A A A\mathcal{A}A, объединение которых совпадает с Ω Ω Omega\OmegaΩ, и пусть ( x k ) k ≥ 1 x k k ≥ 1 (x_(k))_(k >= 1)\left(x_{k}\right)_{k \geq 1}(xk)k≥1 счетное семейство из R R RRR. Тогда отображение ξ : Ω → R ξ : Ω → R xi:Omega rarr R\xi: \Omega \rightarrow Rξ:Ω→R, определяемое равенством
ξ ( ω ) = ∑ k ≥ 1 x k I A k ( ω ) ξ ( ω ) = ∑ k ≥ 1   x k I A k ( ω ) xi(omega)=sum_(k >= 1)x_(k)I_(A_(k))(omega)\xi(\omega)=\sum_{k \geq 1} x_{k} I_{A_{k}}(\omega)ξ(ω)=∑k≥1xkIAk(ω)
будет случайной величиной на измеримом пространстве ( Ω , A Ω , A Omega,A\Omega, \mathcal{A}Ω,A ).
(1.2.3) Каждое непрерывное отображение вида ξ : R v → R ξ : R v → R xi:R^(v)rarr R\xi: R^{v} \rightarrow Rξ:Rv→R является случайной величиной на измеримом пространстве ( R v , B v R v , B v R^(v),B^(v)R^{v}, \mathcal{B}^{v}Rv,Bv ).
(1.2.4) Множество случайных величин замкнуто относительно основных операций анализа: сложения, вычитания, умножения, деления при отличном от нуля делителя и предельного перехода).
(1.2.5) Пусть v v vvv - некоторое натуральное число и ( ξ ( k ) ) 1 ≤ k ≤ v ξ ( k ) 1 ≤ k ≤ v (xi^((k)))_(1 <= k <= v)\left(\xi^{(k)}\right)_{1 \leq k \leq v}(ξ(k))1≤k≤v - набор отображений вида Ω → R Ω → R Omega rarr R\Omega \rightarrow RΩ→R. Для того, чтобы векторное отображение ξ : Ω → R v ξ : Ω → R v xi:Omega rarrR^(v)\xi: \Omega \rightarrow R^{v}ξ:Ω→Rv, определяемое равенством
ξ ( ω ) = ( ξ 1 ( ω ) , … , ξ v ( ω ) ) , ξ ( ω ) = ξ 1 ( ω ) , … , ξ v ( ω ) , xi(omega)=(xi_(1)(omega),dots,xi_(v)(omega)),\xi(\omega)=\left(\xi_{1}(\omega), \ldots, \xi_{v}(\omega)\right),ξ(ω)=(ξ1(ω),…,ξv(ω)),
было векторной случайной величиной необходимо и достаточно, чтобы каждое отображение ξ ( k ) , 1 ≤ k ≤ v ξ ( k ) , 1 ≤ k ≤ v xi^((k)),1 <= k <= v\xi^{(k)}, 1 \leq k \leq vξ(k),1≤k≤v, было скалярной случайной величиной.
Пусть ( Ω , A , P Ω , A , P Omega,A,P\Omega, \mathcal{A}, PΩ,A,P ) - вероятностное пространство, B v B v B^(v)\mathcal{B}^{v}Bv - борелевская σ σ sigma\sigmaσ-алгебра на R v R v R^(v)R^{v}Rv. Каждая случайная величина ξ : Ω → R v ξ : Ω → R v xi:Omega rarrR^(v)\xi: \Omega \rightarrow R^{v}ξ:Ω→Rv определяет на борелевской σ σ sigma\sigmaσ-алгебре B v B v B^(v)\mathcal{B}^{v}Bv отображение P ξ : B v → R P ξ : B v → R P_(xi):B^(v)rarr RP_{\xi}: \mathcal{B}^{v} \rightarrow RPξ:Bv→R при помощи равенства
P ξ ( B ) = P ( ξ − 1 ( B ) ) = P ( ω ∈ Ω : ξ ( ω ) ∈ B ) , B ∈ B v P ξ ( B ) = P ξ − 1 ( B ) = P ( ω ∈ Ω : ξ ( ω ) ∈ B ) , B ∈ B v P_(xi)(B)=P(xi^(-1)(B))=P(omega in Omega:xi(omega)in B),B inB^(v)P_{\xi}(B)=P\left(\xi^{-1}(B)\right)=P(\omega \in \Omega: \xi(\omega) \in B), B \in \mathcal{B}^{v}Pξ(B)=P(ξ−1(B))=P(ω∈Ω:ξ(ω)∈B),B∈Bv
которое является вероятностью на ( R v , B v R v , B v R^(v),B^(v)R^{v}, \mathcal{B}^{v}Rv,Bv ). Из определения P ξ P ξ P_(xi)P_{\xi}Pξ следует, что P ξ ( B ) ≥ 0 P ξ ( B ) ≥ 0 P_(xi)(B) >= 0P_{\xi}(B) \geq 0Pξ(B)≥0 для любого B ∈ B v B ∈ B v B inB^(v)B \in \mathcal{B}^{v}B∈Bv. Справедливость аксиомы P ξ ( R v ) = 1 P ξ R v = 1 P_(xi)(R^(v))=1P_{\xi}\left(R^{v}\right)=1Pξ(Rv)=1 вытекает из очевидного равенства
ξ − 1 ( R v ) = { ω ∈ Ω : ξ ( ω ) ∈ R v } = Ω . ξ − 1 R v = ω ∈ Ω : ξ ( ω ) ∈ R v = Ω . xi^(-1)(R^(v))={omega in Omega:xi(omega)inR^(v)}=Omega.\xi^{-1}\left(R^{v}\right)=\left\{\omega \in \Omega: \xi(\omega) \in R^{v}\right\}=\Omega .ξ−1(Rv)={ω∈Ω:ξ(ω)∈Rv}=Ω.
Наконец, справедливость равенства
P ξ ( ∑ k ≥ 1 B k ) = ∑ k ≥ 1 P ξ ( B k ) P ξ ∑ k ≥ 1   B k = ∑ k ≥ 1   P ξ B k P_(xi)(sum_(k >= 1)B_(k))=sum_(k >= 1)P_(xi)(B_(k))P_{\xi}\left(\sum_{k \geq 1} B_{k}\right)=\sum_{k \geq 1} P_{\xi}\left(B_{k}\right)Pξ(∑k≥1Bk)=∑k≥1Pξ(Bk)
для любого счетного семейства ( B k ) k ≥ 1 B k k ≥ 1 (B_(k))_(k >= 1)\left(B_{k}\right)_{k \geq 1}(Bk)k≥1 попарно непересекающихся подмножеств из B v B v B^(v)B^{v}Bv следует из тождества
ξ − 1 ( ⋃ k ≥ 1 B k ) = ⋃ k ≥ 1 ξ − 1 ( B k ) ξ − 1 ⋃ k ≥ 1   B k = ⋃ k ≥ 1   ξ − 1 B k xi^(-1)(uuu_(k >= 1)B_(k))=uuu_(k >= 1)xi^(-1)(B_(k))\xi^{-1}\left(\bigcup_{k \geq 1} B_{k}\right)=\bigcup_{k \geq 1} \xi^{-1}\left(B_{k}\right)ξ−1(⋃k≥1Bk)=⋃k≥1ξ−1(Bk)
Вероятность P ξ P ξ P_(xi)P_{\xi}Pξ на борелевской σ σ sigma\sigmaσ-алгебре B v B v B^(v)B^{v}Bv называется распределением вероятностей или просто распределением случайной величины ξ ξ xi\xiξ.
Отображение f : R v → R f : R v → R f:R^(v)rarr Rf: R^{v} \rightarrow Rf:Rv→R называется измеримым по Борелю или борелевским, если для любого борелевского множества B ∈ B v B ∈ B v B inB^(v)B \in \mathcal{B}^{v}B∈Bv множество
f − 1 ( B ) = { x ∈ R v : f ( x ) ∈ B } f − 1 ( B ) = x ∈ R v : f ( x ) ∈ B f^(-1)(B)={x inR^(v):f(x)in B}f^{-1}(B)=\left\{x \in R^{v}: f(x) \in B\right\}f−1(B)={x∈Rv:f(x)∈B}
является борелевским.
(1.2.6) Пусть ξ ξ xi\xiξ - векторная случайная величина на ( Ω , A ) , f : R v → R Ω , A ) , f : R v → R Omega,A),f:R^(v)rarr R\Omega, \mathcal{A}), f: R^{v} \rightarrow RΩ,A),f:Rv→R борелевское отображение. Тогда отображение η : Ω → R v η : Ω → R v eta:Omega rarrR^(v)\eta: \Omega \rightarrow R^{v}η:Ω→Rv, определяемое равенством
η ( ω ) = f ( ξ ( ω ) ) , η ( ω ) = f ( ξ ( ω ) ) , eta(omega)=f(xi(omega)),\eta(\omega)=f(\xi(\omega)),η(ω)=f(ξ(ω)),
является случайной величиной на ( Ω , A Ω , A Omega,A\Omega, \mathcal{A}Ω,A ).
Доказательство. Для любого борелевского подмножества B ∈ B v B ∈ B v B inB^(v)B \in \mathcal{B}^{v}B∈Bv получаем
η − 1 ( B ) = { ω ∈ Ω : η ( ω ) ∈ B } = { ω ∈ Ω : f ( ξ ( ω ) ) ∈ B } = { ω ∈ Ω : ξ ( ω ) ∈ f − 1 ( B ) } = ξ − 1 ( f − 1 ( B ) . η − 1 ( B ) = { ω ∈ Ω : η ( ω ) ∈ B } = { ω ∈ Ω : f ( ξ ( ω ) ) ∈ B } = ω ∈ Ω : ξ ( ω ) ∈ f − 1 ( B ) = ξ − 1 f − 1 ( B ) . {:[eta^(-1)(B)={omega in Omega:eta(omega)in B}={omega in Omega:f(xi(omega))in B}=],[{omega in Omega:xi(omega)inf^(-1)(B)}=xi^(-1)(f^(-1)(B).:}]:}\begin{gathered} \eta^{-1}(B)=\{\omega \in \Omega: \eta(\omega) \in B\}=\{\omega \in \Omega: f(\xi(\omega)) \in B\}= \\ \left\{\omega \in \Omega: \xi(\omega) \in f^{-1}(B)\right\}=\xi^{-1}\left(f^{-1}(B) .\right. \end{gathered}η−1(B)={ω∈Ω:η(ω)∈B}={ω∈Ω:f(ξ(ω))∈B}={ω∈Ω:ξ(ω)∈f−1(B)}=ξ−1(f−1(B).
Так как f f fff борелевское отображение, то f − 1 ( B ) f − 1 ( B ) f^(-1)(B)f^{-1}(B)f−1(B) борелевское множество. ξ ξ xi\xiξ -
случайная величина, поэтому прообраз ξ − 1 ( f − 1 ( B ) ) ξ − 1 f − 1 ( B ) xi^(-1)(f^(-1)(B))\xi^{-1}\left(f^{-1}(B)\right)ξ−1(f−1(B)) борелевского множества f − 1 ( B ) f − 1 ( B ) f^(-1)(B)f^{-1}(B)f−1(B) является событием из A A A\mathcal{A}A. Что и требовалось доказать.
Определенное выше отображение η η eta\etaη называется обычно суперпозицией отображений f f fff и ξ ξ xi\xiξ и обозначается f ∘ ξ f ∘ ξ f@xif \circ \xif∘ξ или f ( ξ ) f ( ξ ) f(xi)f(\xi)f(ξ).
Векторная ( v v vvv-мерная) случайная величина ξ ξ xi\xiξ называется дискретной, если существует не более, чем счетное подмножество Q ξ ⊂ R v Q ξ ⊂ R v Q_(xi)subR^(v)Q_{\xi} \subset R^{v}Qξ⊂Rv, такое, что P ξ ( { x } ) > 0 P ξ ( { x } ) > 0 P_(xi)({x}) > 0P_{\xi}(\{x\})>0Pξ({x})>0 для любого x ∈ Q ξ x ∈ Q ξ x inQ_(xi)x \in Q_{\xi}x∈Qξ и что P ξ ( Q ξ ) = 1 P ξ Q ξ = 1 P_(xi)(Q_(xi))=1P_{\xi}\left(Q_{\xi}\right)=1Pξ(Qξ)=1. Подмножество Q ξ Q ξ Q_(xi)Q_{\xi}Qξ является борелевским и называется множеством значений случайной величины ξ ξ xi\xiξ. Из равенства
P ξ ( R v ) = P ξ ( Q ξ ) + P ξ ( Q ξ C ) = 1 P ξ R v = P ξ Q ξ + P ξ Q ξ C = 1 P_(xi)(R^(v))=P_(xi)(Q_(xi))+P_(xi)(Q_(xi)^(C))=1P_{\xi}\left(R^{v}\right)=P_{\xi}\left(Q_{\xi}\right)+P_{\xi}\left(Q_{\xi}^{C}\right)=1Pξ(Rv)=Pξ(Qξ)+Pξ(QξC)=1
следует, что P ξ ( Q ξ C ) = 0 P ξ Q ξ C = 0 P_(xi)(Q_(xi)^(C))=0P_{\xi}\left(Q_{\xi}^{C}\right)=0Pξ(QξC)=0. Поэтому P ξ ( { x } ) = 0 P ξ ( { x } ) = 0 P_(xi)({x})=0P_{\xi}(\{x\})=0Pξ({x})=0 для каждого x ∈ Q ξ C x ∈ Q ξ C x inQ_(xi)^(C)x \in Q_{\xi}^{C}x∈QξC. Более того, для любого B ∈ B v B ∈ B v B inB^(v)B \in \mathcal{B}^{v}B∈Bv справедливо равенство
P ξ ( B ) = P ξ ( B ∩ Q ξ + B ∩ Q ξ C ) = P ξ ( B ∩ Q ξ ) . P ξ ( B ) = P ξ B ∩ Q ξ + B ∩ Q ξ C = P ξ B ∩ Q ξ . P_(xi)(B)=P_(xi)(B nnQ_(xi)+B nnQ_(xi)^(C))=P_(xi)(B nnQ_(xi)).P_{\xi}(B)=P_{\xi}\left(B \cap Q_{\xi}+B \cap Q_{\xi}^{C}\right)=P_{\xi}\left(B \cap Q_{\xi}\right) .Pξ(B)=Pξ(B∩Qξ+B∩QξC)=Pξ(B∩Qξ).
Следовательно
P ξ ( B ) = ∑ x ∈ B ∩ Q ξ P ξ ( { x } ) . P ξ ( B ) = ∑ x ∈ B ∩ Q ξ   P ξ ( { x } ) . P_(xi)(B)=sum_(x in B nnQ_(xi))P_(xi)({x}).P_{\xi}(B)=\sum_{x \in B \cap Q_{\xi}} P_{\xi}(\{x\}) .Pξ(B)=∑x∈B∩QξPξ({x}).
Пусть ξ ξ xi\xiξ - μ μ mu\muμ-мерная, η − v η − v eta-v\eta-vη−v - мерная дискретные случайные величины, принимающие значения в конечных подмножествах Q μ Q μ Q_(mu)Q_{\mu}Qμ и Q v Q v Q_(v)Q_{v}Qv - конечные подмножества в R μ R μ R^(mu)R^{\mu}Rμ и R v R v R^(v)R^{v}Rv соответственно, а ξ − ( μ + v ) ξ − ( μ + v ) xi-(mu+v)\xi-(\mu+v)ξ−(μ+v) - мерная дискретная случайная величина со значениями в множестве Q μ × Q ν Q μ × Q ν Q_(mu)xxQ_(nu)Q_{\mu} \times Q_{\nu}Qμ×Qν из R μ + ν R μ + ν R^(mu+nu)R^{\mu+\nu}Rμ+ν. Тогда
Пусть ξ ξ xi\xiξ - векторная ( v v vvv-мерная) случайная величина, а P ξ P ξ P_(xi)P_{\xi}Pξ - ее распределение. Неотрицательная измеримая по Борелю функция p ξ : R v → R p ξ : R v → R p_(xi):R^(v)rarr Rp_{\xi}: R^{v} \rightarrow Rpξ:Rv→R называется плотностью распределения P ξ P ξ P_(xi)P_{\xi}Pξ случайной величины ξ ξ xi\xiξ, если для любого борелевского множества B ∈ B v B ∈ B v B inB^(v)B \in B^{v}B∈Bv имеет место равенство
P ξ ( B ) = ∫ B p ξ ( x ) d x P ξ ( B ) = ∫ B   p ξ ( x ) d x P_(xi)(B)=int_(B)p_(xi)(x)dxP_{\xi}(B)=\int_{B} p_{\xi}(x) d xPξ(B)=∫Bpξ(x)dx
В курсах теории вероятностей доказывается, что для каждого неотрицательного отображения вида p : R v → R p : R v → R p:R^(v)rarr Rp: R^{v} \rightarrow Rp:Rv→R такого, что
∫ R v p ( x ) d x = 1 ∫ R v   p ( x ) d x = 1 int_(R^(v))p(x)dx=1\int_{R^{v}} p(x) d x=1∫Rvp(x)dx=1
существует случайная величина ξ ξ xi\xiξ, для которой p p ppp является плотностью вероятностей.
Отображение вида
p ( x ) = { 0 , x < a x b − a 0 , b < x , a ≤ x ≤ b , p ( x ) = 0 , x < a x b − a 0 , b < x , a ≤ x ≤ b , p(x)={[0","x < a],[(x)/(b-a)],[0","b < x],a <= x <= b,:}p(x)=\left\{\begin{array}{l} 0, x<a \\ \frac{x}{b-a} \\ 0, b<x \end{array}, a \leq x \leq b,\right.p(x)={0,x<axb−a0,b<x,a≤x≤b,
является плотностью распределения, которое называется равномерным распределением на интервале [ a , b ] [ a , b ] [a,b][a, b][a,b].
Пусть Y = { y 1 , … , y | Y | } Y = y 1 , … , y | Y | Y={y_(1),dots,y_(|Y|)}Y=\left\{y_{1}, \ldots, y_{|Y|}\right\}Y={y1,…,y|Y|} - конечное множество вещественных чисел, в частности Y = { 0 , … , | Y | − 1 } Y = { 0 , … , | Y | − 1 } Y={0,dots,|Y|-1}Y=\{0, \ldots,|Y|-1\}Y={0,…,|Y|−1}. Семейство
p ( y ) = 1 | Y | , y ∈ Y p ( y ) = 1 | Y | , y ∈ Y p(y)=(1)/(|Y|),quad y in Yp(y)=\frac{1}{|Y|}, \quad y \in Yp(y)=1|Y|,y∈Y
неотрицательных чисел является распределением дискретной случайной величины, которое называется равномерным распределением на множестве Y Y YYY.
При решении прикладных задач для описания свойств векторной случайной величины ξ A = ( ξ a ) a ∈ A ξ A = ξ a a ∈ A xi_(A)=(xi_(a))_(a in A)\xi_{A}=\left(\xi_{a}\right)_{a \in A}ξA=(ξa)a∈A довольно часто вместо | A | | A | |A||A||A|-мерного распределения P Y A P Y A P_(Y)^(A)P_{Y}{ }^{A}PYA используют числовые характеристики случайных величин.
Основной числовой характеристикой случайной величины является число, называемое ее средним значением или математическим ожиданием. Пусть P ξ = ( p ξ ( x ) ) x ∈ Y P ξ = p ξ ( x ) x ∈ Y P_(xi)=(p_(xi)(x))_(x in Y)P_{\xi}=\left(p_{\xi}(x)\right)_{x \in Y}Pξ=(pξ(x))x∈Y - распределение дискретной скалярной случайной величины ξ ξ xi\xiξ со значениями в Y Y YYY, а p η p η p_(eta)p_{\eta}pη - плотность распределения случайной величины η η eta\etaη. Тогда их средние значения определяются равенствами
E ξ = ∑ x z ∈ Y x p ξ ( x ) и E η = ∫ R v x p η ( x ) d x E ξ = ∑ x z ∈ Y   x p ξ ( x )  и  E η = ∫ R v   x p η ( x ) d x E xi=sum_(x_(z)in Y)xp_(xi)(x)" и "E eta=int_(R^(v))xp_(eta)(x)dxE \xi=\sum_{x_{z} \in Y} x p_{\xi}(x) \text { и } E \eta=\int_{R^{v}} x p_{\eta}(x) d xEξ=∑xz∈Yxpξ(x) и Eη=∫Rvxpη(x)dx
Ниже перечислены свойства среднего значения, которые будут использоваться далее. Если c − c − c-c-c− константа, то E ( c ) = c , E ( c ξ ) = c E ξ E ( c ) = c , E ( c ξ ) = c E ξ E(c)=c,E(c xi)=cE xiE(c)=c, E(c \xi)=c E \xiE(c)=c,E(cξ)=cEξ,
E ( ξ + η ) = E ξ + E η E ( ξ + η ) = E ξ + E η E(xi+eta)=E xi+E etaE(\xi+\eta)=E \xi+E \etaE(ξ+η)=Eξ+Eη
Если ξ ξ xi\xiξ и η η eta\etaη независимы, то
E ( ξ η ) = E ξ E η E ( ξ η ) = E ξ E η E(xi eta)=E xi E etaE(\xi \eta)=E \xi E \etaE(ξη)=EξEη
Пусть ξ ξ xi\xiξ и η η eta\etaη - случайные величины, тогда при любом вещественном x x xxx выполняется неравенство
E ( | ξ | x + | η | ) 2 = x 2 E ξ 2 + 2 E | ξ η | + E η 2 ≥ 0 E ( | ξ | x + | η | ) 2 = x 2 E ξ 2 + 2 E | ξ η | + E η 2 ≥ 0 E(|xi|x+|eta|)^(2)=x^(2)Exi^(2)+2E|xi eta|+Eeta^(2) >= 0E(|\xi| x+|\eta|)^{2}=x^{2} E \xi^{2}+2 E|\xi \eta|+E \eta^{2} \geq 0E(|ξ|x+|η|)2=x2Eξ2+2E|ξη|+Eη2≥0
и следующего из него неравенство 4 ( E | ξ η | ) 2 − 4 E ξ 2 E η 2 ≤ 0 4 ( E | ξ η | ) 2 − 4 E ξ 2 E η 2 ≤ 0 4(E|xi eta|)^(2)-4Exi^(2)Eeta^(2) <= 04(E|\xi \eta|)^{2}-4 E \xi^{2} E \eta^{2} \leq 04(E|ξη|)2−4Eξ2Eη2≤0. Последнее неравенство, представленное в форме
E | ξ η | ≤ E ( ξ ) 2 E ( η ) 2 E | ξ η | ≤ E ( ξ ) 2 E ( η ) 2 E|xi eta| <= sqrt(E(xi)^(2)E(eta)^(2))E|\xi \eta| \leq \sqrt{E(\xi)^{2} E(\eta)^{2}}E|ξη|≤E(ξ)2E(η)2
получило название неравенства Буняковского- Коши-Шварца и буде использоваться далее.
Еще одной числовой характеристикой случайной величины ξ ξ xi\xiξ со средним значением E ξ E ξ E xiE \xiEξ является число D ξ D ξ D xiD \xiDξ, определяемое равенством
D ξ = E ( ξ − E ξ ) 2 D ξ = E ( ξ − E ξ ) 2 D xi=E(xi-E xi)^(2)D \xi=E(\xi-E \xi)^{2}Dξ=E(ξ−Eξ)2
Оно называется дисперсией ξ ξ xi\xiξ. Из определения дисперсии немедленно следует, что D ξ ≥ 0 , D ξ = E ( ξ ) 2 − ( E ξ ) 2 D ξ ≥ 0 , D ξ = E ( ξ ) 2 − ( E ξ ) 2 D xi >= 0,D xi=E(xi)^(2)-(E xi)^(2)D \xi \geq 0, D \xi=E(\xi)^{2}-(E \xi)^{2}Dξ≥0,Dξ=E(ξ)2−(Eξ)2 и D ( c ξ ) = c 2 D ξ D ( c ξ ) = c 2 D ξ D(c xi)=c^(2)D xiD(c \xi)=c^{2} D \xiD(cξ)=c2Dξ. Кроме того, если ξ ξ xi\xiξ и η η eta\etaη независимы, то
D ( ξ + η ) = D ξ + D η D ( ξ + η ) = D ξ + D η D(xi+eta)=D xi+D etaD(\xi+\eta)=D \xi+D \etaD(ξ+η)=Dξ+Dη
Квадратный корень из дисперсии D ξ D ξ D xiD \xiDξ называется среднеквадратическим отклонением или стандартом случайной величины ξ ξ xi\xiξ и обозначается буквой σ ξ σ ξ sigma_(xi)\sigma_{\xi}σξ или просто σ σ sigma\sigmaσ, когда это не приводит к неопределенности. Следовательно, σ ξ 2 = D ξ σ ξ 2 = D ξ sigma_(xi)^(2)=D xi\sigma_{\xi}^{2}=D \xiσξ2=Dξ.
Приведенное ниже неравенство
P ( | η − m η | ≥ k σ η ) ≤ 1 k 2 P η − m η ≥ k σ η ≤ 1 k 2 P(|eta-m_(eta)| >= ksigma_(eta)) <= (1)/(k^(2))P\left(\left|\eta-m_{\eta}\right| \geq k \sigma_{\eta}\right) \leq \frac{1}{k^{2}}P(|η−mη|≥kση)≤1k2
называется неравенством Чебышева. Оно позволяет оценить величину рассеивания (разброса) значений случайной величины относительно ее среднего значения в единицах стандартного отклонения σ η σ η sigma_(eta)\sigma_{\eta}ση.
Ковариацией случайных величин ξ z ξ z xi_(z)\xi_{z}ξz и ξ t ξ t xi_(t)\xi_{t}ξt со средними значениями m z m z m_(z)m_{z}mz и m t m t m_(t)m_{t}mt соответственно называется число cov ( ξ z , ξ t ) cov ξ z , ξ t cov(xi_(z),xi_(t))\operatorname{cov}\left(\xi_{z}, \xi_{t}\right)cov(ξz,ξt), определяемое равенством
cov ( ξ z , ξ t ) = E ( ξ z − m z ) ( ξ t − m t ) cov ξ z , ξ t = E ξ z − m z ξ t − m t cov(xi_(z),xi_(t))=E(xi_(z)-m_(z))(xi_(t)-m_(t))\operatorname{cov}\left(\xi_{z}, \xi_{t}\right)=E\left(\xi_{z}-m_{z}\right)\left(\xi_{t}-m_{t}\right)cov(ξz,ξt)=E(ξz−mz)(ξt−mt)
Из этого определения следует, что
cov ( ξ z , ξ z ) = σ z 2 и cov ( ξ z , ξ t ) = cov ( ξ t , ξ z ) . cov ξ z , ξ z = σ z 2  и  cov ξ z , ξ t = cov ξ t , ξ z . cov(xi_(z),xi_(z))=sigma_(z)^(2)" и "cov(xi_(z),xi_(t))=cov(xi_(t),xi_(z)).\operatorname{cov}\left(\xi_{z}, \xi_{z}\right)=\sigma_{z}^{2} \text { и } \operatorname{cov}\left(\xi_{z}, \xi_{t}\right)=\operatorname{cov}\left(\xi_{t}, \xi_{z}\right) .cov(ξz,ξz)=σz2 и cov(ξz,ξt)=cov(ξt,ξz).
Если ξ z ξ z xi_(z)\xi_{z}ξz и ξ t ξ t xi_(t)\xi_{t}ξt независимы, то из свойства E ( ξ z ξ t ) = E ξ z E ξ t E ξ z ξ t = E ξ z E ξ t E(xi_(z)xi_(t))=Exi_(z)Exi_(t)E\left(\xi_{z} \xi_{t}\right)=E \xi_{z} E \xi_{t}E(ξzξt)=EξzEξt средних значений следует, что cov ( ξ z , ξ t ) = 0 cov ξ z , ξ t = 0 cov(xi_(z),xi_(t))=0\operatorname{cov}\left(\xi_{z}, \xi_{t}\right)=0cov(ξz,ξt)=0. Обратное утверждение справедливо только для случайных величин с нормальными распределениями.
Нормированным коэффициентом корреляции двух случайных величин ξ z ξ z xi_(z)\xi_{z}ξz и ξ t ξ t xi_(t)\xi_{t}ξt называется число R ( ξ z , ξ t ) R ξ z , ξ t R(xi_(z),xi_(t))R\left(\xi_{z}, \xi_{t}\right)R(ξz,ξt), определяемое равенством
R ( ξ z , ξ t ) = cov ( ξ z , ξ t ) σ z σ t R ξ z , ξ t = cov ξ z , ξ t σ z σ t R(xi_(z),xi_(t))=(cov(xi_(z),xi_(t)))/(sigma_(z)sigma_(t))R\left(\xi_{z}, \xi_{t}\right)=\frac{\operatorname{cov}\left(\xi_{z}, \xi_{t}\right)}{\sigma_{z} \sigma_{t}}R(ξz,ξt)=cov(ξz,ξt)σzσt
С помощью неравенства Буняковского-Коши-Шварца, легко убедиться в том, что | R ( ξ z , ξ t ) | ≤ 1 R ξ z , ξ t ≤ 1 |R(xi_(z),xi_(t))| <= 1\left|R\left(\xi_{z}, \xi_{t}\right)\right| \leq 1|R(ξz,ξt)|≤1. Если ξ z ξ z xi_(z)\xi_{z}ξz и ξ t ξ t xi_(t)\xi_{t}ξt - независимы, то из выше сказанного следует, что R ( ξ z , ξ t ) = 0 R ξ z , ξ t = 0 R(xi_(z),xi_(t))=0R\left(\xi_{z}, \xi_{t}\right)=0R(ξz,ξt)=0. С другой стороны, пусть ξ ξ xi\xiξ - случайная величина со средним E ξ = m E ξ = m E xi=mE \xi=mEξ=m и дисперсией D ξ = σ 2 D ξ = σ 2 D xi=sigma^(2)D \xi=\sigma^{2}Dξ=σ2. Пусть c ≠ 0 c ≠ 0 c!=0c \neq 0c≠0 и d d ddd - вещественные числа и η = c ξ + d η = c ξ + d eta=cxi+d\eta=\mathrm{c} \xi+dη=cξ+d - случайная величина со средним E η = c m + d E η = c m + d E eta=cm+dE \eta=c m+dEη=cm+d и дисперсией D η = c 2 σ 2 D η = c 2 σ 2 D eta=c^(2)sigma^(2)D \eta=c^{2} \sigma^{2}Dη=c2σ2. Тогда
R ( ξ , η ) = E ( ξ − m ) ( c ξ + d − c m + d ) | c | σ 2 = c E ( ξ − m ) 2 | c | σ 2 = c | c | R ( ξ , η ) = E ( ξ − m ) ( c ξ + d − c m + d ) | c | σ 2 = c E ( ξ − m ) 2 | c | σ 2 = c | c | R(xi,eta)=(E(xi-m)(c xi+d-cm+d))/(|c|sigma^(2))=(cE(xi-m)^(2))/(|c|sigma^(2))=(c)/(|c|)R(\xi, \eta)=\frac{E(\xi-m)(c \xi+d-c m+d)}{|c| \sigma^{2}}=\frac{c E(\xi-m)^{2}}{|c| \sigma^{2}}=\frac{c}{|c|}R(ξ,η)=E(ξ−m)(cξ+d−cm+d)|c|σ2=cE(ξ−m)2|c|σ2=c|c|
Таким образом, R ( ξ , η ) = 1 R ( ξ , η ) = 1 R(xi,eta)=1R(\xi, \eta)=1R(ξ,η)=1 при c > 1 c > 1 c > 1c>1c>1 и R ( ξ , η ) = − 1 R ( ξ , η ) = − 1 R(xi,eta)=-1R(\xi, \eta)=-1R(ξ,η)=−1 при c < 1 c < 1 c < 1c<1c<1. Перечисленные свойства коэффициента корреляции позволяют использовать его в качестве меры зависимости между случайными величинами.

Задачи

  1. Определить случайную величину ξ ξ xi\xiξ с равномерным распределением на интервале [ 0 , 1 ] [ 0 , 1 ] [0,1][0,1][0,1] (указать Ω , A , P Ω , A , P Omega,A,P\Omega, A, PΩ,A,P и вид отображения ξ : Ω → R ξ : Ω → R xi:Omega rarr R\xi: \Omega \rightarrow Rξ:Ω→R ).
  2. Определить плотность случайной величины с треугольным распределением...
  3. Определить случайную величину ξ = ( ξ 1 , ξ 2 ) ξ = ξ 1 , ξ 2 xi=(xi_(1),xi_(2))\xi=\left(\xi_{1}, \xi_{2}\right)ξ=(ξ1,ξ2) с равномерным распределением на квадрате [ 0 , 1 ] × [ 0 , 1 ] [ 0 , 1 ] × [ 0 , 1 ] [0,1]xx[0,1][0,1] \times[0,1][0,1]×[0,1] (указать Ω , A , P Ω , A , P Omega,A,P\Omega, A, PΩ,A,P и вид отображения ξ : Ω → R ) ξ : Ω → R ) xi:Omega rarr R)\xi: \Omega \rightarrow R)ξ:Ω→R). Показать, что случайные величины ξ 1 ξ 1 xi_(1)\xi_{1}ξ1 и ξ 2 ξ 2 xi_(2)\xi_{2}ξ2 независимы.
  4. Определить случайную величину ξ = ( ξ 1 , ξ 2 ) ξ = ξ 1 , ξ 2 xi=(xi_(1),xi_(2))\xi=\left(\xi_{1}, \xi_{2}\right)ξ=(ξ1,ξ2) с равномерным распределением на круге B ( 0 , 1 ) = { ( x 1 , x 2 ) ∈ R 2 : x 1 2 + x 2 2 ≤ 1 } B ( 0 , 1 ) = x 1 , x 2 ∈ R 2 : x 1 2 + x 2 2 ≤ 1 B(0,1)={(x_(1),x_(2))inR^(2):x_(1)^(2)+x_(2)^(2) <= 1}B(0,1)=\left\{\left(x_{1}, x_{2}\right) \in R^{2}: x_{1}^{2}+x_{2}^{2} \leq 1\right\}B(0,1)={(x1,x2)∈R2:x12+x22≤1} (указать Ω , A , P Ω , A , P Omega,A,P\Omega, A, PΩ,A,P и вид отображения ξ : Ω → R ξ : Ω → R xi:Omega rarr R\xi: \Omega \rightarrow Rξ:Ω→R ). Показать, что ξ 1 ξ 1 xi_(1)\xi_{1}ξ1 и ξ 2 ξ 2 xi_(2)\xi_{2}ξ2 зависимы.

1.3. Свойства многомерных случайных величин

Пусть n n nnn - натуральное число и ( f j ) 1 ≤ j ≤ n f j 1 ≤ j ≤ n (f_(j))_(1 <= j <= n)\left(f_{j}\right)_{1 \leq j \leq n}(fj)1≤j≤n - семейство отображений вида R n → R R n → R R^(n)rarr R\boldsymbol{R}^{n} \rightarrow \boldsymbol{R}Rn→R. Отображение f : R n → R n f : R n → R n f:R^(n)rarrR^(n)f: \boldsymbol{R}^{n} \rightarrow \boldsymbol{R}^{n}f:Rn→Rn, определяемое равенством
f ( x ) = ( f 1 ( x ) , … , f n ( x ) ) , f ( x ) = f 1 ( x ) , … , f n ( x ) , f(x)=(f_(1)(x),dots,f_(n)(x)),f(x)=\left(f_{1}(x), \ldots, f_{n}(x)\right),f(x)=(f1(x),…,fn(x)),
называется гладким, если все отображения f j , 1 ≤ j ≤ n f j , 1 ≤ j ≤ n f_(j),1 <= j <= nf_{j}, 1 \leq j \leq nfj,1≤j≤n, являются непрерывными и имеют непрерывные частные производные. Пусть f f fff - гладкое отображение. Для любого x ∈ R n x ∈ R n x inR^(n)x \in \boldsymbol{R}^{n}x∈Rn существует квадратная матрица
[ ∂ f 1 ( x ) ∂ x 1 … ∂ f 1 ( x ) ∂ x n … … … ∂ f n ( x ) ∂ x 1 … ∂ f n ( x ) ∂ x n ] ∂ f 1 ( x ) ∂ x 1 … ∂ f 1 ( x ) ∂ x n … … … ∂ f n ( x ) ∂ x 1 … ∂ f n ( x ) ∂ x n [[(delf_(1)(x))/(delx_(1)),dots,(delf_(1)(x))/(delx_(n))],[dots,dots,dots],[(delf_(n)(x))/(delx_(1)),dots,(delf_(n)(x))/(delx_(n))]]\left[\begin{array}{ccc} \frac{\partial f_{1}(x)}{\partial x_{1}} & \ldots & \frac{\partial f_{1}(x)}{\partial x_{n}} \\ \ldots & \ldots & \ldots \\ \frac{\partial f_{n}(x)}{\partial x_{1}} & \ldots & \frac{\partial f_{n}(x)}{\partial x_{n}} \end{array}\right][∂f1(x)∂x1…∂f1(x)∂xn………∂fn(x)∂x1…∂fn(x)∂xn]
порядка n n nnn, элементами которой являются частные производные, вычисленные в x x xxx. Она называется матрицей Якоби, а ее определитель, обозначаемый символом D f ( x ) D f ( x ) Df(x)D f(x)Df(x), - якобианом. Таким образом, каждое гладкое отображение f f fff определяет на множестве R n R n R^(n)\boldsymbol{R}^{n}Rn отображение D f D f DfD fDf вида R n → R R n → R R^(n)rarr R\boldsymbol{R}^{n} \rightarrow \boldsymbol{R}Rn→R, ставящее каждому x x xxx значение D f ( x ) D f ( x ) Df(x)D f(x)Df(x).
Пусть f f fff - гладкое отображение вида R n → R n R n → R n R^(n)rarrR^(n)\boldsymbol{R}^{n} \rightarrow \boldsymbol{R}^{n}Rn→Rn. Если в точке x ∈ R n x ∈ R n x inR^(n)x \in \boldsymbol{R}^{n}x∈Rn якобиан D f ( x ) ≠ 0 D f ( x ) ≠ 0 Df(x)!=0D f(x) \neq 0Df(x)≠0, то в окрестности точки f ( x ) f ( x ) f(x)f(x)f(x) существует гладкое обратное отображение f − 1 f − 1 f^(-1)f^{-1}f−1 и выполняется равенство
D f ( x ) D f − 1 ( f ( x ) ) = 1 . D f ( x ) D f − 1 ( f ( x ) ) = 1 . Df(x)Df^(-1)(f(x))=1.D f(x) D f^{-1}(f(x))=1 .Df(x)Df−1(f(x))=1.
Если гладкое отображение f : R v → R v f : R v → R v f:R^(v)rarrR^(v)f: \boldsymbol{R}^{v} \rightarrow \boldsymbol{R}^{v}f:Rv→Rv является, кроме того, взаимно однозначным, то имеет место формула замены переменных в определенном интеграле
∫ B g ( x ) d x = ∫ f − 1 ( B ) g ( f ( x ) ) | D f ( x ) | d x ∫ B   g ( x ) d x = ∫ f − 1 ( B )   g ( f ( x ) ) | D f ( x ) | d x int_(B)g(x)dx=int_(f^(-1)(B))g(f(x))|Df(x)|dx\int_{B} g(x) d x=\int_{f^{-1}(B)} g(f(x))|D f(x)| d x∫Bg(x)dx=∫f−1(B)g(f(x))|Df(x)|dx
В качестве примера применим эту формулу для вычисления плотности случайной величины η = f ( ξ ) η = f ( ξ ) eta=f(xi)\eta=f(\xi)η=f(ξ).
(1.3.1) Пусть ξ = ( ξ j ) 1 ≤ j ≤ n ξ = ξ j 1 ≤ j ≤ n xi=(xi_(j))_(1 <= j <= n)\xi=\left(\xi_{j}\right)_{1 \leq j \leq n}ξ=(ξj)1≤j≤n - случайный вектор, p ξ : R n → R p ξ : R n → R p_(xi):R^(n)rarr Rp_{\xi}: \boldsymbol{R}^{n} \rightarrow \boldsymbol{R}pξ:Rn→R - его плотность, а f : R n → R n f : R n → R n f:R^(n)rarrR^(n)f: \boldsymbol{R}^{n} \rightarrow \boldsymbol{R}^{n}f:Rn→Rn - гладкое взаимно однозначное отображение. Тогда η = f ( ξ ) η = f ( ξ ) eta=f(xi)\eta= f(\xi)η=f(ξ) также является n n nnn-мерной случайной величиной, а ее плотность p η p η p_(eta)p_{\eta}pη определяется равенством вида
p η ( x ) = p ξ ( f − 1 ( x ) ) | D f − 1 ( x ) | p η ( x ) = p ξ f − 1 ( x ) D f − 1 ( x ) p_(eta)(x)=p_(xi)(f^(-1)(x))|Df^(-1)(x)|p_{\eta}(x)=p_{\xi}\left(f^{-1}(x)\right)\left|D f^{-1}(x)\right|pη(x)=pξ(f−1(x))|Df−1(x)|
Доказательство. Пусть B B BBB - произвольное борелевское множество. Требуется показать, что
P η ( B ) = ∫ B p ξ ( f − 1 ( x ) ) | D f − 1 ( x ) | d x P η ( B ) = ∫ B   p ξ f − 1 ( x ) D f − 1 ( x ) d x P_(eta)(B)=int_(B)p_(xi)(f^(-1)(x))|Df^(-1)(x)|dxP_{\eta}(B)=\int_{B} p_{\xi}\left(f^{-1}(x)\right)\left|D f^{-1}(x)\right| d xPη(B)=∫Bpξ(f−1(x))|Df−1(x)|dx
Для этого вычислим интеграл из правой части равенства, используя замену переменных:
∫ B p ξ ( f − 1 ( x ) ) | D f − 1 ( x ) | d x = ∫ f − 1 ( B ) p ξ ( f − 1 ( f ( x ) ) ) | D f − 1 ( f ( x ) ) | | D f ( x ) | d x = ∫ f − 1 ( B ) p ξ ( x ) d x = P ξ ( f − 1 ( B ) ) ∫ B   p ξ f − 1 ( x ) D f − 1 ( x ) d x = ∫ f − 1 ( B )   p ξ f − 1 ( f ( x ) ) D f − 1 ( f ( x ) ) | D f ( x ) | d x = ∫ f − 1 ( B )   p ξ ( x ) d x = P ξ f − 1 ( B ) {:[int_(B)p_(xi)(f^(-1)(x))|Df^(-1)(x)|dx=],[int_(f^(-1)(B))p_(xi)(f^(-1)(f(x)))|Df^(-1)(f(x))||Df(x)|dx=],[int_(f^(-1)(B))p_(xi)(x)dx=P_(xi)(f^(-1)(B))]:}\begin{gathered} \int_{B} p_{\xi}\left(f^{-1}(x)\right)\left|D f^{-1}(x)\right| d x= \\ \int_{f^{-1}(B)} p_{\xi}\left(f^{-1}(f(x))\right)\left|D f^{-1}(f(x))\right||D f(x)| d x= \\ \int_{f^{-1}(B)} p_{\xi}(x) d x=P_{\xi}\left(f^{-1}(B)\right) \end{gathered}∫Bpξ(f−1(x))|Df−1(x)|dx=∫f−1(B)pξ(f−1(f(x)))|Df−1(f(x))||Df(x)|dx=∫f−1(B)pξ(x)dx=Pξ(f−1(B))
Из определения распределения следует, что для взаимно однозначного и гладкого отображения f f fff
P ξ ( f − 1 ( B ) ) = P { ω ∈ Ω : ξ ( ω ) ∈ f − 1 ( B ) } = P { ω ∈ Ω : f ( ξ ( ω ) ) ∈ ( B ) } = P { ω ∈ Ω : η ( ω ) ∈ B } = P η ( B ) . P ξ f − 1 ( B ) = P ω ∈ Ω : ξ ( ω ) ∈ f − 1 ( B ) = P { ω ∈ Ω : f ( ξ ( ω ) ) ∈ ( B ) } = P { ω ∈ Ω : η ( ω ) ∈ B } = P η ( B ) . {:[P_(xi)(f^(-1)(B))=P{omega in Omega:xi(omega)inf^(-1)(B)}=P{omega in Omega:f(xi(omega))in(B)}=],[P{omega in Omega:eta(omega)in B}=P_(eta)(B).]:}\begin{gathered} P_{\xi}\left(f^{-1}(B)\right)=P\left\{\omega \in \Omega: \xi(\omega) \in f^{-1}(B)\right\}=P\{\omega \in \Omega: f(\xi(\omega)) \in(B)\}= \\ P\{\omega \in \Omega: \eta(\omega) \in B\}=P_{\eta}(B) . \end{gathered}Pξ(f−1(B))=P{ω∈Ω:ξ(ω)∈f−1(B)}=P{ω∈Ω:f(ξ(ω))∈(B)}=P{ω∈Ω:η(ω)∈B}=Pη(B).
Что и требовалось доказать.
(1.3.2) Пусть ξ = ( ξ j ) 1 ≤ j ≤ n ξ = ξ j 1 ≤ j ≤ n xi=(xi_(j))_(1 <= j <= n)\xi=\left(\xi_{j}\right)_{1 \leq j \leq n}ξ=(ξj)1≤j≤n - случайный вектор, p ξ p ξ p_(xi)p_{\xi}pξ - его плотность, а f : R n → R n f : R n → R n f:R^(n)rarrR^(n)f: R^{n} \rightarrow R^{n}f:Rn→Rn - взаимно однозначное отображение. Тогда распределение вектора η = f ( ξ ) η = f ( ξ ) eta=f(xi)\eta=f(\xi)η=f(ξ) имеет плотность p η p η p_(eta)p_{\eta}pη, определяемую равенством
p η ( x ) = p ξ ( f − 1 ( x ) ) | D f − 1 ( x ) | . p η ( x ) = p ξ f − 1 ( x ) D f − 1 ( x ) . p_(eta)(x)=p_(xi)(f^(-1)(x))|Df^(-1)(x)|.p_{\eta}(x)=p_{\xi}\left(f^{-1}(x)\right)\left|D f^{-1}(x)\right| .pη(x)=pξ(f−1(x))|Df−1(x)|.
Доказательство.
∫ B p ξ ( f − 1 ( x ) ) | D f − 1 ( x ) | d x = ∫ f − 1 ( B ) p ξ ( f − 1 ( f ( x ) ) ) | D f − 1 ( f ( x ) ) | | D f ( x ) | d x = ∫ f − 1 ( B ) p ξ ( x ) d x = P { ω : ξ ( ω ) ∈ f − 1 ( B ) } = P { ω : f ( ξ ( ω ) ) ∈ B } = P { ω : η ( ω ) ∈ B } ∫ B   p ξ f − 1 ( x ) D f − 1 ( x ) d x = ∫ f − 1 ( B )   p ξ f − 1 ( f ( x ) ) D f − 1 ( f ( x ) ) | D f ( x ) | d x = ∫ f − 1 ( B )   p ξ ( x ) d x = P ω : ξ ( ω ) ∈ f − 1 ( B ) = P { ω : f ( ξ ( ω ) ) ∈ B } = P { ω : η ( ω ) ∈ B } {:[int_(B)p_(xi)(f^(-1)(x))|Df^(-1)(x)|dx=],[int_(f^(-1)(B))p_(xi)(f^(-1)(f(x)))|Df^(-1)(f(x))||Df(x)|dx=int_(f^(-1)(B))p_(xi)(x)dx=],[P{omega:xi(omega)inf^(-1)(B)}=P{omega:f(xi(omega))in B}=P{omega:eta(omega)in B}]:}\begin{gathered} \int_{B} p_{\xi}\left(f^{-1}(x)\right)\left|D f^{-1}(x)\right| d x= \\ \int_{f^{-1}(B)} p_{\xi}\left(f^{-1}(f(x))\right)\left|D f^{-1}(f(x))\right||D f(x)| d x=\int_{f^{-1}(B)} p_{\xi}(x) d x= \\ P\left\{\omega: \xi(\omega) \in f^{-1}(B)\right\}=P\{\omega: f(\xi(\omega)) \in B\}=P\{\omega: \eta(\omega) \in B\} \end{gathered}∫Bpξ(f−1(x))|Df−1(x)|dx=∫f−1(B)pξ(f−1(f(x)))|Df−1(f(x))||Df(x)|dx=∫f−1(B)pξ(x)dx=P{ω:ξ(ω)∈f−1(B)}=P{ω:f(ξ(ω))∈B}=P{ω:η(ω)∈B}
Матрица C ξ C ξ C_(xi)C_{\xi}Cξ вида
C ξ = [ cov ( ξ 1 , ξ 1 ) … cov ( ξ 1 , ξ n ) … … … cov ( ξ n , ξ 1 ) … cov ( ξ n , ξ n ) ] C ξ = cov ξ 1 , ξ 1 … cov ξ 1 , ξ n … … … cov ξ n , ξ 1 … cov ξ n , ξ n C_(xi)=[[cov(xi_(1),xi_(1)),dots,cov(xi_(1),xi_(n))],[dots,dots,dots],[cov(xi_(n),xi_(1)),dots,cov(xi_(n),xi_(n))]]C_{\xi}=\left[\begin{array}{ccc} \operatorname{cov}\left(\xi_{1}, \xi_{1}\right) & \ldots & \operatorname{cov}\left(\xi_{1}, \xi_{n}\right) \\ \ldots & \ldots & \ldots \\ \operatorname{cov}\left(\xi_{n}, \xi_{1}\right) & \ldots & \operatorname{cov}\left(\xi_{n}, \xi_{n}\right) \end{array}\right]Cξ=[cov(ξ1,ξ1)…cov(ξ1,ξn)………cov(ξn,ξ1)…cov(ξn,ξn)]
называется ковариационной матрицей n − n − n-n-n− мерной случайной величины ξ ξ xi\xiξ.
(1.3.3) Пусть x = ( x j ) 1 ≤ j ≤ n x = x j 1 ≤ j ≤ n x=(x_(j))_(1 <= j <= n)x=\left(x_{j}\right)_{1 \leq j \leq n}x=(xj)1≤j≤n - вектор из R n , ξ = ( ξ j ) 1 ≤ j ≤ n R n , ξ = ξ j 1 ≤ j ≤ n R^(n),xi=(xi_(j))_(1 <= j <= n)\boldsymbol{R}^{n}, \xi=\left(\xi_{j}\right)_{1 \leq j \leq n}Rn,ξ=(ξj)1≤j≤n - векторная
случайная величина, a ( x , ξ ) a ( x , ξ ) a(x,xi)\mathrm{a}(x, \xi)a(x,ξ) - скалярная случайная величина, определяемая равенством вида
( x , ξ ) = ∑ j = 1 n x j ξ j ( x , ξ ) = ∑ j = 1 n   x j ξ j (x,xi)=sum_(j=1)^(n)x_(j)xi_(j)(x, \xi)=\sum_{j=1}^{n} x_{j} \xi_{j}(x,ξ)=∑j=1nxjξj
Тогда D ( x , ξ ) = ( C ξ x , x ) D ( x , ξ ) = C ξ x , x D(x,xi)=(C_(xi)x,x)D(x, \xi)=\left(C_{\xi} x, x\right)D(x,ξ)=(Cξx,x).
Доказательство. Так как
E ( x , ξ ) = ∑ j = 1 n x j m j E ( x , ξ ) = ∑ j = 1 n   x j m j E(x,xi)=sum_(j=1)^(n)x_(j)m_(j)E(x, \xi)=\sum_{j=1}^{n} x_{j} m_{j}E(x,ξ)=∑j=1nxjmj
то из определения дисперсии следует, что
D ( x , ξ ) = E ( ∑ j = 1 n x j ξ j − ∑ j = 1 n x j m j ) 2 = E ( ∑ i = 1 n x i ( ξ i − m i ) ) 2 = E ( ∑ i = 1 n ∑ j = 1 n x i ( ξ i − m i ) x j ( ξ j − m j ) ) = ∑ i = 1 n ∑ j = 1 n cov ( ξ i , ξ j ) x i x j ∑ i = 1 n ( ∑ j = 1 n cov ( ξ i , ξ j ) x j ) x i = ∑ i = 1 ( C ξ x ) i x i = ( C ξ x , x ) D ( x , ξ ) = E ∑ j = 1 n   x j ξ j − ∑ j = 1 n   x j m j 2 = E ∑ i = 1 n   x i ξ i − m i 2 = E ∑ i = 1 n   ∑ j = 1 n   x i ξ i − m i x j ξ j − m j = ∑ i = 1 n   ∑ j = 1 n   cov ξ i , ξ j x i x j ∑ i = 1 n   ∑ j = 1 n   cov ξ i , ξ j x j x i = ∑ i = 1   C ξ x i x i = C ξ x , x {:[D(x","xi)=E(sum_(j=1)^(n)x_(j)xi_(j)-sum_(j=1)^(n)x_(j)m_(j))^(2)=E(sum_(i=1)^(n)x_(i)(xi_(i)-m_(i)))^(2)=],[E(sum_(i=1)^(n)sum_(j=1)^(n)x_(i)(xi_(i)-m_(i))x_(j)(xi_(j)-m_(j)))=sum_(i=1)^(n)sum_(j=1)^(n)cov(xi_(i),xi_(j))x_(i)x_(j)],[sum_(i=1)^(n)(sum_(j=1)^(n)cov(xi_(i),xi_(j))x_(j))x_(i)=sum_(i=1)(C_(xi)x)_(i)x_(i)=(C_(xi)x,x)]:}\begin{gathered} D(x, \xi)=E\left(\sum_{j=1}^{n} x_{j} \xi_{j}-\sum_{j=1}^{n} x_{j} m_{j}\right)^{2}=E\left(\sum_{i=1}^{n} x_{i}\left(\xi_{i}-m_{i}\right)\right)^{2}= \\ E\left(\sum_{i=1}^{n} \sum_{j=1}^{n} x_{i}\left(\xi_{i}-m_{i}\right) x_{j}\left(\xi_{j}-m_{j}\right)\right)=\sum_{i=1}^{n} \sum_{j=1}^{n} \operatorname{cov}\left(\xi_{i}, \xi_{j}\right) x_{i} x_{j} \\ \sum_{i=1}^{n}\left(\sum_{j=1}^{n} \operatorname{cov}\left(\xi_{i}, \xi_{j}\right) x_{j}\right) x_{i}=\sum_{i=1}\left(C_{\xi} x\right)_{i} x_{i}=\left(C_{\xi} x, x\right) \end{gathered}D(x,ξ)=E(∑j=1nxjξj−∑j=1nxjmj)2=E(∑i=1nxi(ξi−mi))2=E(∑i=1n∑j=1nxi(ξi−mi)xj(ξj−mj))=∑i=1n∑j=1ncov(ξi,ξj)xixj∑i=1n(∑j=1ncov(ξi,ξj)xj)xi=∑i=1(Cξx)ixi=(Cξx,x)
Теорема доказана. Из нее следует, в частности, что ковариационная матрица C ξ C ξ C_(xi)C_{\xi}Cξ любой векторной случайной величины ξ = ( ξ j ) 1 ≤ j ≤ n ξ = ξ j 1 ≤ j ≤ n xi=(xi_(j))_(1 <= j <= n)\xi=\left(\xi_{j}\right)_{1 \leq j \leq n}ξ=(ξj)1≤j≤n является неотрицательно определенной. В самом деле, ( C ξ x , x ) = D ( x , ξ ) ≥ 0 C ξ x , x = D ( x , ξ ) ≥ 0 (C_(xi)x,x)=D(x,xi) >= 0\left(C_{\xi} x, x\right)=D(x, \xi) \geq 0(Cξx,x)=D(x,ξ)≥0 для любого x ∈ R n x ∈ R n x inR^(n)x \in \boldsymbol{R}^{n}x∈Rn.
Пусть ξ = ( ξ j ) 1 ≤ j ≤ n ξ = ξ j 1 ≤ j ≤ n xi=(xi_(j))_(1 <= j <= n)\xi=\left(\xi_{j}\right)_{1 \leq j \leq n}ξ=(ξj)1≤j≤n - векторная случайная величина. Говорят, что ее распределение P ξ P ξ P_(xi)P_{\xi}Pξ сосредоточено на множестве Q Q QQQ из R n R n R^(n)\boldsymbol{R}^{n}Rn, если P ξ ( Q ) = 1 P ξ ( Q ) = 1 P_(xi)(Q)=1P_{\xi}(Q)=1Pξ(Q)=1.
Пусть q ∈ R , a = ( a j ) 1 ≤ j ≤ n q ∈ R , a = a j 1 ≤ j ≤ n q in R,a=(a_(j))_(1 <= j <= n)q \in \boldsymbol{R}, a=\left(a_{j}\right)_{1 \leq j \leq n}q∈R,a=(aj)1≤j≤n - вектор из R n ∖ { 0 } R n ∖ { 0 } R^(n)\\{0}\boldsymbol{R}^{n} \backslash\{0\}Rn∖{0}. Подмножество H H HHH из R n R n R^(n)\boldsymbol{R}^{n}Rn, определяемое равенством
H = { x ∈ R n : ( a , x ) = q } , H = x ∈ R n : ( a , x ) = q , H={x inR^(n):(a,x)=q},H=\left\{x \in \boldsymbol{R}^{n}:(a, x)=q\right\},H={x∈Rn:(a,x)=q},
называется гиперплоскостью.
(1.3.4) Пусть ξ = ( ξ j ) 1 ≤ j ≤ n ξ = ξ j 1 ≤ j ≤ n xi=(xi_(j))_(1 <= j <= n)\xi=\left(\xi_{j}\right)_{1 \leq j \leq n}ξ=(ξj)1≤j≤n - векторная случайная величина. Для того, чтобы ее распределение P ξ P ξ P_(xi)P_{\xi}Pξ было сосредоточено на некоторой гиперплоскости H ⊂ R n H ⊂ R n H subR^(n)H \subset \boldsymbol{R}^{n}H⊂Rn необходимо и достаточно, чтобы ковариационная матрица C ξ C ξ C_(xi)C_{\xi}Cξ была вырожденной.
Доказательство необходимости. Пусть H H HHH - гиперплоскость, на которой сосредоточено распределение P ξ P ξ P_(xi)P_{\xi}Pξ. Тогда из P ξ ( H ) = 1 P ξ ( H ) = 1 P_(xi)(H)=1P_{\xi}(H)=1Pξ(H)=1 следует, что
P ( ξ − 1 ( H ) ) = P { ω ∈ Ω : ξ ( ω ) ∈ H } = P { ω ∈ Ω : ( a , ξ ( ω ) ) = q } = 1 . P ξ − 1 ( H ) = P { ω ∈ Ω : ξ ( ω ) ∈ H } = P { ω ∈ Ω : ( a , ξ ( ω ) ) = q } = 1 . P(xi^(-1)(H))=P{omega in Omega:xi(omega)in H}=P{omega in Omega:(a,xi(omega))=q}=1.P\left(\xi^{-1}(H)\right)=P\{\omega \in \Omega: \xi(\omega) \in H\}=P\{\omega \in \Omega:(a, \xi(\omega))=q\}=1 .P(ξ−1(H))=P{ω∈Ω:ξ(ω)∈H}=P{ω∈Ω:(a,ξ(ω))=q}=1.
Следовательно, скалярная случайная величина ( a , ξ ) ( a , ξ ) (a,xi)(a, \xi)(a,ξ) принимает с вероятностью равной единице значение q q qqq. Это означает, что ее дисперсия D ( a , ξ ) = 0 D ( a , ξ ) = 0 D(a,xi)=0D(a, \xi)=0D(a,ξ)=0. Из (1.3.2) следует, что ( C ξ a , a ) = 0 C ξ a , a = 0 (C_(xi)a,a)=0\left(C_{\xi} a, a\right)=0(Cξa,a)=0 при a ∈ R n ∖ { 0 } a ∈ R n ∖ { 0 } a inR^(n)\\{0}a \in \boldsymbol{R}^{n} \backslash\{0\}a∈Rn∖{0}. Если квадратичная форма обращается в ноль при ненулевом векторе a ∈ R n ∖ { 0 } a ∈ R n ∖ { 0 } a inR^(n)\\{0}a \in \boldsymbol{R}^{n} \backslash\{0\}a∈Rn∖{0}, то ее матрица C ξ C ξ C_(xi)C_{\xi}Cξ называется вырожденной.
Достаточность. Пусть ковариационная матрица C ξ C ξ C_(xi)C_{\xi}Cξ - вырождена. Тогда существует такое a ∈ R n ∖ { 0 } a ∈ R n ∖ { 0 } a inR^(n)\\{0}a \in R^{n} \backslash\{0\}a∈Rn∖{0}, что ( C ξ a , a ) = 0 C ξ a , a = 0 (C_(xi)a,a)=0\left(C_{\xi} a, a\right)=0(Cξa,a)=0. Из (2.3.2) следует, что дисперсия D ( a , ξ ) = 0 D ( a , ξ ) = 0 D(a,xi)=0D(a, \xi)=0D(a,ξ)=0. Это означает, что существует q ∈ R q ∈ R q in Rq \in \boldsymbol{R}q∈R такое, что вероятность равенства ( a , ξ ) = q ( a , ξ ) = q (a,xi)=q(a, \xi)=q(a,ξ)=q равна единице. То есть
P { ω ∈ Ω : ( a , ξ ( ω ) ) = q } = P ( { ω ∈ Ω : ξ ( ω ) ∈ H } = P ( ξ − 1 ( H ) ) = P ξ ( H ) = 1 . P { ω ∈ Ω : ( a , ξ ( ω ) ) = q } = P { ω ∈ Ω : ξ ( ω ) ∈ H } = P ξ − 1 ( H ) = P ξ ( H ) = 1 . P{omega in Omega:(a,xi(omega))=q}=P({omega in Omega:xi(omega)in H}=P(xi^(-1)(H))=P_(xi)(H)=1.:}P\{\omega \in \Omega:(a, \xi(\omega))=q\}=P\left(\{\omega \in \Omega: \xi(\omega) \in H\}=P\left(\xi^{-1}(H)\right)=P_{\xi}(H)=1 .\right.P{ω∈Ω:(a,ξ(ω))=q}=P({ω∈Ω:ξ(ω)∈H}=P(ξ−1(H))=Pξ(H)=1.
Теорема доказана.
(1.3.5) Пусть ξ = ( ξ j ) 1 ≤ j ≤ n − n ξ = ξ j 1 ≤ j ≤ n − n xi=(xi_(j))_(1 <= j <= n)-n\xi=\left(\xi_{j}\right)_{1 \leq j \leq n}-nξ=(ξj)1≤j≤n−n-мерная случайная величина, C ξ − C ξ − C_(xi)-C_{\xi}-Cξ− ее матрица ковариаций, a = ( a j ) 1 ≤ j ≤ m a = a j 1 ≤ j ≤ m a=(a_(j))_(1 <= j <= m)a=\left(a_{j}\right)_{1 \leq j \leq m}a=(aj)1≤j≤m - вектор из R m R m R^(m)\boldsymbol{R}^{m}Rm и A = ( a i j ) 1 ≤ i ≤ m , 1 ≤ j ≤ n A = a i j 1 ≤ i ≤ m , 1 ≤ j ≤ n A=(a_(ij))_(1 <= i <= m,1 <= j <= n)A=\left(a_{i j}\right)_{1 \leq i \leq m, 1 \leq j \leq n}A=(aij)1≤i≤m,1≤j≤n матрица размерности m × n m × n m xx nm \times nm×n. Тогда η = A ξ + a η = A ξ + a eta=A xi+a\eta=A \xi+aη=Aξ+a является m m mmm-мерной случайной величиной с матрицей ковариации
C η = A C ξ A t . C η = A C ξ A t . C_(eta)=AC_(xi)A^(t).C_{\eta}=A C_{\xi} A^{t} .Cη=ACξAt.
Доказательство. Для любого i , 1 ≤ i ≤ m i , 1 ≤ i ≤ m i,1 <= i <= mi, 1 \leq i \leq mi,1≤i≤m, отображение f i : R n → R f i : R n → R f_(i):R^(n)rarr Rf_{i}: \boldsymbol{R}^{n} \rightarrow \boldsymbol{R}fi:Rn→R, определяемое равенством
f i ( x ) = ∑ j = 1 n a i j x j + a i , f i ( x ) = ∑ j = 1 n   a i j x j + a i , f_(i)(x)=sum_(j=1)^(n)a_(ij)x_(j)+a_(i),f_{i}(x)=\sum_{j=1}^{n} a_{i j} x_{j}+a_{i},fi(x)=∑j=1naijxj+ai,
является непрерывной функцией. Поэтому η i = f i ( ξ ) η i = f i ( ξ ) eta_(i)=f_(i)(xi)\eta_{i}=f_{i}(\xi)ηi=fi(ξ) - скалярная случайная величина, а η = A ξ + a η = A ξ + a eta=A xi+a\eta=A \xi+aη=Aξ+a - векторная. Используя (2.3.2), для каждого x ∈ R n x ∈ R n x inR^(n)x \in \boldsymbol{R}^{n}x∈Rn получаем
D ( x , η ) = D ( x , A ξ + a ) = 0 + D ( x , A ξ ) = D ( x , A ξ ) . D ( x , η ) = D ( x , A ξ + a ) = 0 + D ( x , A ξ ) = D ( x , A ξ ) . D(x,eta)=D(x,A xi+a)=0+D(x,A xi)=D(x,A xi).D(x, \eta)=D(x, A \xi+a)=0+D(x, A \xi)=D(x, A \xi) .D(x,η)=D(x,Aξ+a)=0+D(x,Aξ)=D(x,Aξ).
Из непосредственно проверяемого тождества ( x , A y ) = ( A t x , y ) ( x , A y ) = A t x , y (x,Ay)=(A^(t)x,y)(x, A y)=\left(A^{t} x, y\right)(x,Ay)=(Atx,y), где x x xxx и y y yyy векторы из R n R n R^(n)\boldsymbol{R}^{n}Rn, а A A AAA - квадратная матрица порядка n n nnn, следует, что
D ( x , η ) = D ( A t x , ξ ) = ( C ξ A t x , A t x ) = ( A C ξ A t x , x ) . D ( x , η ) = D A t x , ξ = C ξ A t x , A t x = A C ξ A t x , x . D(x,eta)=D(A^(t)x,xi)=(C_(xi)A^(t)x,A^(t)x)=(AC_(xi)A^(t)x,x).D(x, \eta)=D\left(A^{t} x, \xi\right)=\left(C_{\xi} A^{t} x, A^{t} x\right)=\left(A C_{\xi} A^{t} x, x\right) .D(x,η)=D(Atx,ξ)=(CξAtx,Atx)=(ACξAtx,x).
С другой стороны, на основании (2.3.2) имеем равенство D ( x , η ) = ( C η x , x ) D ( x , η ) = C η x , x D(x,eta)=(C_(eta)x,x)D(x, \eta)=\left(C_{\eta} x, x\right)D(x,η)=(Cηx,x), из которого следует утверждение теоремы.
Задачи
  1. Пусть x x xxx и y y yyy векторы из R n R n R^(n)\boldsymbol{R}^{n}Rn, а A A AAA - квадратная матрица порядка n n nnn. Доказать тождество ( x , A y ) = ( A t x , y ) ( x , A y ) = A t x , y (x,Ay)=(A^(t)x,y)(x, A y)=\left(A^{t} x, y\right)(x,Ay)=(Atx,y).

1.4. Многомерное нормальное распределение

Говорят, что одномерная случайная величина ξ ξ xi\xiξ имеет стандартное одномерное нормальное распределение, если его плотность p ξ p ξ p_(xi)p_{\xi}pξ определяется равенCTBOM
p ξ ( x ) = 1 2 π e − x 2 2 . p ξ ( x ) = 1 2 π e − x 2 2 . p_(xi)(x)=(1)/(sqrt(2pi))e^(-(x^(2))/(2)).p_{\xi}(x)=\frac{1}{\sqrt{2 \pi}} e^{-\frac{x^{2}}{2}} .pξ(x)=12πe−x22.
Непосредственным вычислением можно убедиться в том, что ее среднее значение E ξ = 0 E ξ = 0 E xi=0E \xi=0Eξ=0, а дисперсия D ξ = 1 D ξ = 1 D xi=1D \xi=1Dξ=1. Если η = σ ξ + a η = σ ξ + a eta=sigma xi+a\eta=\sigma \xi+aη=σξ+a, то E η = a E η = a E eta=aE \eta=aEη=a и D η = σ 2 D η = σ 2 D eta=sigma^(2)D \eta=\sigma^{2}Dη=σ2. Распределение случайной величины η η eta\etaη называется одномерным нормальным распределением с параметрами N ( a , σ ) N ( a , σ ) N(a,sigma)N(a, \sigma)N(a,σ). Из (1.3.2) следует, что плотность ее распределения имеет вид
p η ( x ) = 1 σ p ξ ( x − a σ ) = 1 σ 2 π e − 1 2 ( x − a σ ) 2 . p η ( x ) = 1 σ p ξ x − a σ = 1 σ 2 π e − 1 2 x − a σ 2 . p_(eta)(x)=(1)/(sigma)p_(xi)((x-a)/(sigma))=(1)/(sigmasqrt(2pi))e^(-(1)/(2)((x-a)/(sigma))^(2)).p_{\eta}(x)=\frac{1}{\sigma} p_{\xi}\left(\frac{x-a}{\sigma}\right)=\frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{1}{2}\left(\frac{x-a}{\sigma}\right)^{2}} .pη(x)=1σpξ(x−aσ)=1σ2πe−12(x−aσ)2.
Распределение n n nnn-мерного случайного вектора ξ = ( ξ j ) 1 ≤ j ≤ n ξ = ξ j 1 ≤ j ≤ n xi=(xi_(j))_(1 <= j <= n)\boldsymbol{\xi}=\left(\xi_{j}\right)_{1 \leq j \leq n}ξ=(ξj)1≤j≤n с независимыми компонентами принято называть n n nnn-мерным стандартным нормальным распределением, если каждая одномерная компонента имеет стандартное нормальное распределение с параметрами N ( 0 , 1 ) N ( 0 , 1 ) N(0,1)N(0,1)N(0,1). В этом случае
p ξ ( x ) = ∏ j = 1 n p ξ j ( x j ) = ∏ j = 1 n 1 2 π e − x j 2 2 = 1 ( 2 π ) n e − ( x , x ) 2 , p ξ ( x ) = ∏ j = 1 n   p ξ j x j = ∏ j = 1 n   1 2 π e − x j 2 2 = 1 ( 2 π ) n e − ( x , x ) 2 , p_(xi)(x)=prod_(j=1)^(n)p_(xi_(j))(x_(j))=prod_(j=1)^(n)(1)/(sqrt(2pi))e^(-(x_(j)^(2))/(2))=(1)/((sqrt(2pi))^(n))e^(-((x,x))/(2)),p_{\xi}(x)=\prod_{j=1}^{n} p_{\xi_{j}}\left(x_{j}\right)=\prod_{j=1}^{n} \frac{1}{\sqrt{2 \pi}} e^{-\frac{x_{j}^{2}}{2}}=\frac{1}{(\sqrt{2 \pi})^{n}} e^{-\frac{(\boldsymbol{x}, \boldsymbol{x})}{2}},pξ(x)=∏j=1npξj(xj)=∏j=1n12πe−xj22=1(2π)ne−(x,x)2,
а матрица ковариаций C ξ = E C ξ = E C_(xi)=EC_{\xi}=ECξ=E. В самом деле, если i ≠ j i ≠ j i!=ji \neq ji≠j, то cov ( ξ i , ξ j ) = E ξ i E ξ j = 0 cov ξ i , ξ j = E ξ i E ξ j = 0 cov(xi_(i),xi_(j))=Exi_(i)Exi_(j)=0\operatorname{cov}\left(\xi_{i}, \xi_{j}\right)= E \xi_{i} E \xi_{j}=0cov(ξi,ξj)=EξiEξj=0, в остальных случаях cov ( ξ i , ξ i ) = E ( ξ i ) 2 = 1 cov ξ i , ξ i = E ξ i 2 = 1 cov(xi_(i),xi_(i))=E(xi_(i))^(2)=1\operatorname{cov}\left(\xi_{i}, \xi_{i}\right)=E\left(\xi_{i}\right)^{2}=1cov(ξi,ξi)=E(ξi)2=1.
Пусть A A AAA - квадратная матрица порядка n , ξ = ( ξ j ) 1 ≤ j ≤ n n , ξ = ξ j 1 ≤ j ≤ n n,xi=(xi_(j))_(1 <= j <= n)n, \boldsymbol{\xi}=\left(\xi_{j}\right)_{1 \leq j \leq n}n,ξ=(ξj)1≤j≤n - случайный вектор со стандартным нормальным распределением и a ∈ R n a ∈ R n a inR^(n)\boldsymbol{a} \in \boldsymbol{R}^{n}a∈Rn. Распределение случайного вектора η = ( η j ) 1 ≤ j ≤ n η = η j 1 ≤ j ≤ n eta=(eta_(j))_(1 <= j <= n)\boldsymbol{\eta}=\left(\eta_{j}\right)_{1 \leq j \leq n}η=(ηj)1≤j≤n, определяемого равенством η = A ξ + a η = A ξ + a eta=A xi+a\boldsymbol{\eta}=A \boldsymbol{\xi}+\boldsymbol{a}η=Aξ+a, называется n n nnn-мерным нормальным распределением. Так как
η j = ∑ k = 1 n a j k ξ k + a j , 1 ≤ j ≤ n , η j = ∑ k = 1 n   a j k ξ k + a j , 1 ≤ j ≤ n , eta_(j)=sum_(k=1)^(n)a_(jk)xi_(k)+a_(j),1 <= j <= n,\eta_{j}=\sum_{k=1}^{n} a_{j k} \xi_{k}+a_{j}, 1 \leq j \leq n,ηj=∑k=1najkξk+aj,1≤j≤n,
то E η j = a j E η j = a j Eeta_(j)=a_(j)E \eta_{j}=a_{j}Eηj=aj. Так как C ξ = E C ξ = E C_(xi)=EC_{\xi}=ECξ=E, то из (1.3.5) следует, что C η = A C ξ A t = A A t C η = A C ξ A t = A A t C_(eta)=AC_(xi)A^(t)=AA^(t)C_{\eta}=A C_{\xi} A^{t}=A A^{t}Cη=ACξAt=AAt.
(1.4.1) Если ξ = ( ξ j ) 1 ≤ j ≤ n ξ = ξ j 1 ≤ j ≤ n xi=(xi_(j))_(1 <= j <= n)\boldsymbol{\xi}=\left(\xi_{j}\right)_{1 \leq j \leq n}ξ=(ξj)1≤j≤n - случайный вектор со стандартным n n nnn-мерным нормальным распределением, а η = A ξ + a η = A ξ + a eta=A xi+a\boldsymbol{\eta}=A \boldsymbol{\xi}+\boldsymbol{a}η=Aξ+a, то плотность p η n p η n p_(eta)np_{\boldsymbol{\eta}} npηn-мерного нормального распределения случайного вектора η η eta\boldsymbol{\eta}η имеет вид
p η ( x ) = 1 ( 2 π ) n det ( C η ) exp ⁡ ( − 1 2 ( C η − 1 ( x − a ) , ( x − a ) ) ) . p η ( x ) = 1 ( 2 π ) n det C η exp ⁡ − 1 2 C η − 1 ( x − a ) , ( x − a ) . p_(eta)(x)=(1)/((sqrt(2pi))^(n)sqrt(det(C_(eta))))exp(-(1)/(2)(C_(eta)^(-1)(x-a),(x-a))).p_{\boldsymbol{\eta}}(\boldsymbol{x})=\frac{1}{(\sqrt{2 \pi})^{n} \sqrt{\operatorname{det}\left(C_{\boldsymbol{\eta}}\right)}} \exp \left(-\frac{1}{2}\left(C_{\boldsymbol{\eta}}^{-1}(\boldsymbol{x}-\boldsymbol{a}),(\boldsymbol{x}-\boldsymbol{a})\right)\right) .pη(x)=1(2π)ndet(Cη)exp⁡(−12(Cη−1(x−a),(x−a))).
Доказательство. Покажем, что отображение f ( x ) = A x + a f ( x ) = A x + a f(x)=Ax+af(x)=A x+af(x)=Ax+a вида R n → R n R n → R n R^(n)rarrR^(n)\boldsymbol{R}^{n} \rightarrow \boldsymbol{R}^{n}Rn→Rn является гладким взаимно однозначным и воспользуемся для вычисления p η p η p_(eta)p_{\eta}pη теоремой (1.3.1). Из нее следует, что
p η ( x ) = p ξ ( f − 1 ( x ) ) | D f − 1 ( x ) | p η ( x ) = p ξ f − 1 ( x ) D f − 1 ( x ) p_(eta)(x)=p_(xi)(f^(-1)(x))|Df^(-1)(x)|p_{\eta}(x)=p_{\xi}\left(f^{-1}(x)\right)\left|D f^{-1}(x)\right|pη(x)=pξ(f−1(x))|Df−1(x)|
Так как для любого i , 1 ≤ i ≤ n i , 1 ≤ i ≤ n i,1 <= i <= ni, 1 \leq i \leq ni,1≤i≤n, отображения f j : R n → R f j : R n → R f_(j):R^(n)rarr Rf_{j}: R^{n} \rightarrow Rfj:Rn→R, определяемые равенством
f i ( x ) = ∑ k = 1 n a i k x k + a i f i ( x ) = ∑ k = 1 n   a i k x k + a i f_(i)(x)=sum_(k=1)^(n)a_(ik)x_(k)+a_(i)f_{i}(x)=\sum_{k=1}^{n} a_{i k} x_{k}+a_{i}fi(x)=∑k=1naikxk+ai
непрерывны вместе со своими производными
∂ f i ( x ) ∂ x j = a i j ∂ f i ( x ) ∂ x j = a i j (delf_(i)(x))/(delx_(j))=a_(ij)\frac{\partial f_{i}(x)}{\partial x_{j}}=a_{i j}∂fi(x)∂xj=aij
то f f fff является гладким. Поэтому в каждой точке x ∈ R n x ∈ R n x inR^(n)x \in R^{n}x∈Rn Якобиан отображения f = ( f j ) 1 ≤ j ≤ n f = f j 1 ≤ j ≤ n f=(f_(j))_(1 <= j <= n)f=\left(f_{j}\right)_{1 \leq j \leq n}f=(fj)1≤j≤n равен D f ( x ) = det ( A ) D f ( x ) = det ( A ) Df(x)=det(A)D f(x)=\operatorname{det}(A)Df(x)=det(A). При det ( A ) ≠ 0 det ( A ) ≠ 0 det(A)!=0\operatorname{det}(A) \neq 0det(A)≠0 прообраз любого x ∈ R n x ∈ R n x inR^(n)x \in \boldsymbol{R}^{n}x∈Rn
f − 1 ( x ) = { t ∈ R n : A t + a = x } = { t ∈ R n : t = A − 1 ( x − a ) } = A − 1 ( x − a ) f − 1 ( x ) = t ∈ R n : A t + a = x = t ∈ R n : t = A − 1 ( x − a ) = A − 1 ( x − a ) f^(-1)(x)={t inR^(n):At+a=x}={t inR^(n):t=A^(-1)(x-a)}=A^(-1)(x-a)f^{-1}(x)=\left\{t \in \boldsymbol{R}^{n}: A t+a=x\right\}=\left\{t \in \boldsymbol{R}^{n}: t=A^{-1}(x-a)\right\}=A^{-1}(x-a)f−1(x)={t∈Rn:At+a=x}={t∈Rn:t=A−1(x−a)}=A−1(x−a)
является вектор A − 1 ( x − a ) A − 1 ( x − a ) A^(-1)(x-a)A^{-1}(x-a)A−1(x−a), то отображение f f fff является взаимно однозначным. Из D f ( x ) = det ( A ) D f ( x ) = det ( A ) Df(x)=det(A)D f(x)=\operatorname{det}(A)Df(x)=det(A) и D f ( x ) D f − 1 ( f ( x ) ) = 1 D f ( x ) D f − 1 ( f ( x ) ) = 1 Df(x)Df^(-1)(f(x))=1D f(x) D f^{-1}(f(x))=1Df(x)Df−1(f(x))=1 следует, что
| D f − 1 ( f ( x ) ) | = 1 | det ( A ) | D f − 1 ( f ( x ) ) = 1 | det ( A ) | |Df^(-1)(f(x))|=(1)/(|det(A)|)\left|D f^{-1}(f(x))\right|=\frac{1}{|\operatorname{det}(A)|}|Df−1(f(x))|=1|det(A)|
С другой стороны, det ( C η ) = det ( A ) ( det A t ) = ( det ( A ) ) 2 det C η = det ( A ) det A t = ( det ( A ) ) 2 det(C_(eta))=det(A)(detA^(t))=(det(A))^(2)\operatorname{det}\left(C_{\eta}\right)=\operatorname{det}(A)\left(\operatorname{det} A^{t}\right)=(\operatorname{det}(A))^{2}det(Cη)=det(A)(detAt)=(det(A))2. Поэтому det ( A ) = det ( C η ) det ( A ) = det C η det(A)=sqrt(det(C_(eta)))\operatorname{det}(A)=\sqrt{\operatorname{det}\left(C_{\eta}\right)}det(A)=det(Cη). Применяя (2.3.1), получаем
p η ( x ) = 1 ( 2 π ) n det C η exp ⁡ ( − 1 2 ( A − 1 ( x − a ) , A − 1 ( x − a ) ) ) . p η ( x ) = 1 ( 2 π ) n det C η exp ⁡ − 1 2 A − 1 ( x − a ) , A − 1 ( x − a ) . p_(eta)(x)=(1)/((sqrt(2pi))^(n)sqrt(detC_(eta)))exp(-(1)/(2)(A^(-1)(x-a),A^(-1)(x-a))).p_{\eta}(x)=\frac{1}{(\sqrt{2 \pi})^{n} \sqrt{\operatorname{det} C_{\eta}}} \exp \left(-\frac{1}{2}\left(A^{-1}(x-a), A^{-1}(x-a)\right)\right) .pη(x)=1(2π)ndetCηexp⁡(−12(A−1(x−a),A−1(x−a))).
После применения известного тождества ( x , A y ) = ( A t x , y ) ) ( x , A y ) = A t x , y {:(x,Ay)=(A^(t)x,y))\left.(x, A y)=\left(A^{t} x, y\right)\right)(x,Ay)=(Atx,y)), где x x xxx и y y yyy векторы из R n R n R^(n)\boldsymbol{R}^{n}Rn, а A A AAA - квадратная матрица порядка n n nnn, к скалярному произведению из правой части, имеем
( A − 1 ( x − a ) , A − 1 ( x − a ) ) = ( ( A − 1 ) t A − 1 ( x − a ) , ( x − a ) ) . A − 1 ( x − a ) , A − 1 ( x − a ) = A − 1 t A − 1 ( x − a ) , ( x − a ) . (A^(-1)(x-a),A^(-1)(x-a))=((A^(-1))^(t)A^(-1)(x-a),(x-a)).\left(A^{-1}(x-a), A^{-1}(x-a)\right)=\left(\left(A^{-1}\right)^{t} A^{-1}(x-a),(x-a)\right) .(A−1(x−a),A−1(x−a))=((A−1)tA−1(x−a),(x−a)).
Транспонируя равенство A A − 1 = E A A − 1 = E AA^(-1)=EA A^{-1}=EAA−1=E, имеем ( A − 1 ) t A t = E A − 1 t A t = E (A^(-1))^(t)A^(t)=E\left(A^{-1}\right)^{t} A^{t}=E(A−1)tAt=E. После умножения обеих его частей справа на ( A t ) − 1 A t − 1 (A^(t))^(-1)\left(A^{t}\right)^{-1}(At)−1 получаем равенство ( A − 1 ) t = ( A t ) − 1 A − 1 t = A t − 1 (A^(-1))^(t)=(A^(t))^(-1)\left(A^{-1}\right)^{t}=\left(A^{t}\right)^{-1}(A−1)t=(At)−1. Поэтому
( A − 1 ) t A − 1 = ( A t ) − 1 A − 1 = ( A A t ) − 1 = C η − 1 A − 1 t A − 1 = A t − 1 A − 1 = A A t − 1 = C η − 1 (A^(-1))^(t)A^(-1)=(A^(t))^(-1)A^(-1)=(AA^(t))^(-1)=C_(eta)^(-1)\left(A^{-1}\right)^{t} A^{-1}=\left(A^{t}\right)^{-1} A^{-1}=\left(A A^{t}\right)^{-1}=C_{\eta}^{-1}(A−1)tA−1=(At)−1A−1=(AAt)−1=Cη−1
Это позволяет записать скалярное произведение из правой части последнего равенства в нужном виде
( C η − 1 ( x − a ) , ( x − a ) ) , C η − 1 ( x − a ) , ( x − a ) , (C_(eta)^(-1)(x-a),(x-a)),\left(C_{\eta}^{-1}(x-a),(x-a)\right),(Cη−1(x−a),(x−a)),
чем и завершается доказательство.
Таким образом, n n nnn-мерное нормальное распределение случайного вектора η η eta\etaη определяется его вектором a a aaa средних значений и ковариационной матрицей C η C η C_(eta)C_{\eta}Cη и кратко обозначается N ( a , C η ) N a , C η N(a,C_(eta))N\left(a, C_{\eta}\right)N(a,Cη). Если det ( C η ) = 0 det C η = 0 det(C_(eta))=0\operatorname{det}\left(C_{\eta}\right)=0det(Cη)=0, то из (2.3.3) следует, что нормальное распределение сосредоточено на гиперплоскости. В этом случае плотность p η p η p_(eta)p_{\eta}pη распределения в R n R n R^(n)\boldsymbol{R}^{n}Rn не существует.

Задачи

  1. Пусть ξ ξ xi\xiξ - случайный вектор с n n nnn-мерным нормальным распределением N ( a , C ξ ) , B N a , C ξ , B N(a,C_(xi)),BN\left(a, C_{\xi}\right), BN(a,Cξ),B - матрица размерности m × n m × n m xx nm \times nm×n и b ∈ R m b ∈ R m b inR^(m)b \in R^{m}b∈Rm. Показать, что случайный вектор η = B ξ + b η = B ξ + b eta=B xi+b\eta=B \xi+bη=Bξ+b имеет нормальное m m mmm-мерное распределение с параметрами N ( B a + b , C ξ B C ξ t ) N B a + b , C ξ B C ξ t N(Ba+b,C_(xi)BC_(xi)^(t))N\left(B a+b, C_{\xi} B C_{\xi}^{t}\right)N(Ba+b,CξBCξt).

1.5 Бесконечные семейства случайных величин и теорема Колмогорова

Пусть ( Ω , A , P Ω , A , P Omega,A,P\Omega, \mathcal{A}, PΩ,A,P ) - вероятностное пространство, Z 2 Z 2 Z^(2)Z^{2}Z2 - двумерная целочисленная решетка, C ⊂ Z 2 C ⊂ Z 2 C subZ^(2)C \subset Z^{2}C⊂Z2 и ξ C = ( ξ c ) c ∈ C ξ C = ξ c c ∈ C xi_(C)=(xi_(c))_(c in C)\xi_{C}=\left(\xi_{c}\right)_{c \in C}ξC=(ξc)c∈C - векторная ( | C | | C | |C||C||C|-мерная) случайная величина. Ее значениями являются, очевидно, наборы x C x C x_(C)x_{C}xC из множества
Y C = { x C = ( x c ) c ∈ C : x c ∈ Y , c ∈ C } . Y C = x C = x c c ∈ C : x c ∈ Y , c ∈ C . Y^(C)={x_(C)=(x_(c))_(c in C):x_(c)in Y,quad c in C}.Y^{C}=\left\{x_{C}=\left(x_{c}\right)_{c \in C}: x_{c} \in Y, \quad c \in C\right\} .YC={xC=(xc)c∈C:xc∈Y,c∈C}.
Для каждого x C = ( x c ) c ∈ C x C = x c c ∈ C x_(C)=(x_(c))_(c in C)x_{C}=\left(x_{c}\right)_{c \in C}xC=(xc)c∈C из Y C Y C Y^(C)Y^{C}YC его вероятность p Y c ( x C ) p Y c x C p_(Y)c(x_(C))p_{Y} c\left(x_{C}\right)pYc(xC) определяется равенством
p Y c ( x C ) = P ( ω ∈ Ω : ξ C ( ω ) = x C ) . p Y c x C = P ω ∈ Ω : ξ C ( ω ) = x C . p_(Y)c(x_(C))=P(omega in Omega:xi_(C)(omega)=x_(C)).p_{Y} c\left(x_{C}\right)=P\left(\omega \in \Omega: \xi_{C}(\omega)=x_{C}\right) .pYc(xC)=P(ω∈Ω:ξC(ω)=xC).
Из определения дискретной случайной величины следует, что
∑ x C ∈ Y p Y c ( x C ) = ⋯ = 1 . ∑ x C ∈ Y   p Y c x C = ⋯ = 1 . sum_(x_(C)in Y)p_(Y)c(x_(C))=cdots=1.\sum_{x_{C} \in Y} p_{Y} c\left(x_{C}\right)=\cdots=1 .∑xC∈YpYc(xC)=⋯=1.
Распределение вероятностей P Y C = ( p Y c ( x C ) ) x C ∈ Y P Y C = p Y c x C x C ∈ Y P_(Y)C=(p_(Y)c(x_(C)))_(x_(C)in Y)P_{Y} C=\left(p_{Y} c\left(x_{C}\right)\right)_{x_{C} \in Y}PYC=(pYc(xC))xC∈Y с векторной случайной величины ξ C ξ C xi_(C)\xi_{C}ξC принято называть конечномерным распределением.
Пусть A A AAA - подмножество C C CCC, а B = C ∖ A B = C ∖ A B=C\\AB=C \backslash AB=C∖A. Тогда ξ A = ( ξ a ) a ∈ A ξ A = ξ a a ∈ A xi_(A)=(xi_(a))_(a in A)\xi_{A}=\left(\xi_{a}\right)_{a \in A}ξA=(ξa)a∈A и ξ B = ( ξ b ) b ∈ B ξ B = ξ b b ∈ B xi_(B)=(xi_(b))_(b in B)\xi_{B}= \left(\xi_{b}\right)_{b \in B}ξB=(ξb)b∈B - также векторные случайные величины со значениями в Y A Y A Y^(A)Y^{A}YA и Y B Y B Y^(B)Y^{B}YB и распределениями P Y A = ( p Y A ( x A ) ) x A ∈ Y A P Y A = p Y A x A x A ∈ Y A P_(Y^(A))=(p_(Y^(A))(x_(A)))_(x_(A)inY^(A))P_{Y^{A}}=\left(p_{Y^{A}}\left(x_{A}\right)\right)_{x_{A} \in Y^{A}}PYA=(pYA(xA))xA∈YA и P Y B = ( p Y B ( x B ) ) x B ∈ Y B P Y B = p Y B x B x B ∈ Y B P_(Y^(B))=(p_(Y^(B))(x_(B)))_(x_(B)inY^(B))P_{Y^{B}}=\left(p_{Y^{B}}\left(x_{B}\right)\right)_{x_{B} \in Y^{B}}PYB=(pYB(xB))xB∈YB. Так как C = A + B , x C = ( x A , x B ) C = A + B , x C = x A , x B C=A+B,x_(C)=(x_(A),x_(B))C= A+B, x_{C}=\left(x_{A}, x_{B}\right)C=A+B,xC=(xA,xB), то имеет место равенство
p Y A ( x A ) = ∑ x B ∈ Y B p Y A + B ( x A + B ) . p Y A x A = ∑ x B ∈ Y B   p Y A + B x A + B . p_(Y^(A))(x_(A))=sum_(x_(B)inY^(B))p_(Y^(A+B))(x_(A+B)).p_{Y^{A}}\left(x_{A}\right)=\sum_{x_{B} \in Y^{B}} p_{Y^{A+B}}\left(x_{A+B}\right) .pYA(xA)=∑xB∈YBpYA+B(xA+B).
Пусть каждому конечному подмножеству C C CCC из Z 2 Z 2 Z^(2)Z^{2}Z2 поставлено в соответствие распределение вероятностей P Y c = ( p Y c ( x C ) ) x C ∈ Y P Y c = p Y c x C x C ∈ Y P_(Y)c=(p_(Y)c(x_(C)))_(x_(C)in Y)P_{Y} c=\left(p_{Y} c\left(x_{C}\right)\right)_{x_{C} \in Y}PYc=(pYc(xC))xC∈Y. Конечномерные распределения, образующие семейство называются согласованными, если для них выполняется указанное выше равенство.
Семейство ( ξ z ) z ∈ Z 2 ξ z z ∈ Z 2 (xi_(z))_(z inZ^(2))\left(\xi_{z}\right)_{z \in Z^{2}}(ξz)z∈Z2 дискретных случайных величин, определенных на ( Ω , A ) ( Ω , A ) (Omega,A)(\Omega, \mathcal{A})(Ω,A), со значениями в конечном множестве Y Y YYY называется случайным полем на Z 2 Z 2 Z^(2)Z^{2}Z2. В 1933 году вышла книга А.Н. Колмогорова с названием «Основные понятия теории вероятностей». В ней доказана теорема, в которой утверждается, что перечисленные выше условия являются не только необходимыми, но и достаточными для существования случайного поля. Применительно к рассматриваемому случаю ее формулировка выглядит следующим образом.
(1.5.1) Пусть Y Y YYY - конечное подмножество из R R RRR, и пусть каждому конечному подмножеству A ⊂ Z 2 A ⊂ Z 2 A subZ^(2)A \subset Z^{2}A⊂Z2 поставлено в соответствие конечномерное распределение вероятностей P Y A = ( p Y A ( x A ) ) x A ∈ Y A P Y A = p Y A x A x A ∈ Y A P_(Y^(A))=(p_(Y^(A))(x_(A)))_(x_(A)inY^(A))P_{Y^{A}}=\left(p_{Y^{A}}\left(x_{A}\right)\right)_{x_{A} \in Y^{A}}PYA=(pYA(xA))xA∈YA на Y A Y A Y^(A)Y^{A}YA. Если эти распределения
являются согласованными, то существует случайное поле ( ξ z ) z ∈ Z 2 ξ z z ∈ Z 2 (xi_(z))_(z inZ^(2))\left(\xi_{z}\right)_{z \in Z^{2}}(ξz)z∈Z2 такое, что для любого x A = ( x a ) a ∈ A x A = x a a ∈ A x_(A)=(x_(a))_(a in A)x_{A}=\left(x_{a}\right)_{a \in A}xA=(xa)a∈A выполняется равенство
P ( ω ∈ Ω : ξ A ( ω ) = x A ) = p Y A ( x A ) . P ω ∈ Ω : ξ A ( ω ) = x A = p Y A x A . P(omega in Omega:xi_(A)(omega)=x_(A))=p_(Y^(A))(x_(A)).P\left(\omega \in \Omega: \xi_{A}(\omega)=x_{A}\right)=p_{Y^{A}}\left(x_{A}\right) .P(ω∈Ω:ξA(ω)=xA)=pYA(xA).
Доказательство теоремы Колмогорова можно найти в работах [XXX]. В следующем подразделе предлагается пример ее применения.
При любом фиксированном ω ∈ Ω ω ∈ Ω omega in Omega\omega \in \Omegaω∈Ω каждая случайная величина ξ z , z ∈ Z 2 ξ z , z ∈ Z 2 xi_(z),z inZ^(2)\xi_{z}, z \in Z^{2}ξz,z∈Z2, принимает некоторое значение x z = ξ z ( ω ) x z = ξ z ( ω ) x_(z)=xi_(z)(omega)x_{z}=\xi_{z}(\omega)xz=ξz(ω) из Y Y YYY. Таким образом, каждое ω ∈ Ω ω ∈ Ω omega in Omega\omega \in \Omegaω∈Ω определяет семейство x = ( x z ) z ∈ Z 2 x = x z z ∈ Z 2 x=(x_(z))_(z inZ^(2))x=\left(x_{z}\right)_{z \in Z^{2}}x=(xz)z∈Z2. Оно называется реализацией или выборочной поверхностью случайного поля.

1.6 Примеры случайных полей

Очевидно, что распределение P Y A = ( p Y A ( x A ) ) x A ∈ Y A P Y A = p Y A x A x A ∈ Y A P_(Y^(A))=(p_(Y^(A))(x_(A)))_(x_(A)inY^(A))P_{Y^{A}}=\left(p_{Y^{A}}\left(x_{A}\right)\right)_{x_{A} \in Y^{A}}PYA=(pYA(xA))xA∈YA на Y A Y A Y^(A)Y^{A}YA состоит из | Y | | A | | Y | | A | |Y|^(|A|)|Y|^{|A|}|Y||A| вероятностей. При решении прикладных задач априорные сведения о свойствах сцены, необходимые для определения вероятностей, образующих распределение P Y A P Y A P_(Y)^(A)P_{Y}{ }^{A}PYA, часто отсутствуют. В этих условиях приходится идти на различные ограничения. Одним из таких ограничений может быть предположение о независимости случайных величин, образующих поле ( ξ z ) z ∈ Z 2 ξ z z ∈ Z 2 (xi_(z))_(z inZ^(2))\left(\xi_{z}\right)_{z \in Z^{2}}(ξz)z∈Z2. Оно позволяет представить вероятность p Y A ( x A ) p Y A x A p_(Y^(A))(x_(A))p_{Y^{A}}\left(x_{A}\right)pYA(xA) в виде произведения из | A | | A | |A||A||A| вероятностей p Y { a } ( x a ) , a ∈ A p Y { a } x a , a ∈ A p_(Y){a}(x_(a)),a in Ap_{Y}\{a\}\left(x_{a}\right), a \in ApY{a}(xa),a∈A :
p Y A ( x A ) = ∏ a ∈ A p Y { a } ( x a ) . p Y A x A = ∏ a ∈ A   p Y { a } x a . p_(Y^(A))(x_(A))=prod_(a in A)p_(Y^({a}))(x_(a)).p_{Y^{A}}\left(x_{A}\right)=\prod_{a \in A} p_{Y^{\{a\}}}\left(x_{a}\right) .pYA(xA)=∏a∈ApY{a}(xa).
Очевидно, что для задания распределения P Y { a } = ( p Y { a } ( y ) ) y ∈ Y P Y { a } = p Y { a } ( y ) y ∈ Y P_(Y^({a}))=(p_(Y^({a}))(y))_(y in Y)P_{Y^{\{a\}}}=\left(p_{Y^{\{a\}}}(y)\right)_{y \in Y}PY{a}=(pY{a}(y))y∈Y случайной величины ξ a , a ∈ A ξ a , a ∈ A xi_(a),a in A\xi_{a}, a \in Aξa,a∈A, требуется всего | Y | | Y | |Y||Y||Y| вероятностей. Поэтому для задания распределения P Y A = ( p Y A ( x A ) ) x A ∈ Y A P Y A = p Y A x A x A ∈ Y A P_(Y^(A))=(p_(Y^(A))(x_(A)))_(x_(A)inY^(A))P_{Y^{A}}=\left(p_{Y^{A}}\left(x_{A}\right)\right)_{x_{A} \in Y^{A}}PYA=(pYA(xA))xA∈YA на множестве Y A Y A Y^(A)Y^{A}YA требуется | A | | Y | | A | | Y | |A||Y||A||Y||A||Y| вероятностей вида p Y { a } ( x a ) p Y { a } x a p_(Y^({a}))(x_(a))p_{Y^{\{a\}}}\left(x_{a}\right)pY{a}(xa) вместо | Y | | A | | Y | | A | |Y|^(|A|)|Y|^{|A|}|Y||A| вероятностей p Y A ( x A ) p Y A x A p_(Y^(A))(x_(A))p_{Y^{A}}\left(x_{A}\right)pYA(xA).
Осталось только убедиться в том, что определенный выше набор неотрицательных чисел p Y A ( x A ) p Y A x A p_(Y^(A))(x_(A))p_{Y^{A}}\left(x_{A}\right)pYA(xA) на самом деле является конечномерным распределением на Y A Y A Y^(A)Y^{A}YA и для семейства всех таких распределений выполняются условия согласованности. Покажем вначале, что
∑ x A ∈ Y A p Y A ( x A ) = 1 . ∑ x A ∈ Y A   p Y A x A = 1 . sum_(x_(A)inY^(A))p_(Y^(A))(x_(A))=1.\sum_{x_{A} \in Y^{A}} p_{Y^{A}}\left(x_{A}\right)=1 .∑xA∈YApYA(xA)=1.
В самом деле
∑ x A ∈ Y A ( ∏ a ∈ A p Y { a } ( x a ) ) = ∑ x b ∈ Y , b ∈ A ∖ { a } ∑ x a ∈ Y ( p Y { a } ( x a ) ∏ b ∈ A ∖ { a } p Y { b } ( x b ) ) = ∑ x b ∈ Y , b ∈ A ∖ { a } ∏ b ∈ A ∖ { a } p Y { b } ( x b ) ∑ x a ∈ Y p Y { a } ( x a ) = ∑ x b ∈ Y , b ∈ A ∖ { a } ∏ b ∈ A ∖ { a } p Y { b } ( x b ) ∑ x A ∈ Y A   ∏ a ∈ A   p Y { a } x a = ∑ x b ∈ Y , b ∈ A ∖ { a }   ∑ x a ∈ Y   p Y { a } x a ∏ b ∈ A ∖ { a }   p Y { b } x b = ∑ x b ∈ Y , b ∈ A ∖ { a }   ∏ b ∈ A ∖ { a }   p Y { b } x b ∑ x a ∈ Y   p Y { a } x a = ∑ x b ∈ Y , b ∈ A ∖ { a }   ∏ b ∈ A ∖ { a }   p Y { b } x b {:[sum_(x_(A)inY^(A))(prod_(a in A)p_(Y^({a}))(x_(a)))=sum_(x_(b)in Y,b in A\\{a})sum_(x_(a)in Y)(p_(Y^({a}))(x_(a))prod_(b in A\\{a})p_(Y^({b}))(x_(b)))=],[sum_(x_(b)in Y,b in A\\{a})prod_(b in A\\{a})p_(Y^({b}))(x_(b))sum_(x_(a)in Y)p_(Y^({a}))(x_(a))=sum_(x_(b)in Y,b in A\\{a})prod_(b in A\\{a})p_(Y^({b}))(x_(b))]:}\begin{gathered} \sum_{x_{A} \in Y^{A}}\left(\prod_{a \in A} p_{Y^{\{a\}}}\left(x_{a}\right)\right)=\sum_{x_{b} \in Y, b \in A \backslash\{a\}} \sum_{x_{a} \in Y}\left(p_{Y^{\{a\}}}\left(x_{a}\right) \prod_{b \in A \backslash\{a\}} p_{Y^{\{b\}}}\left(x_{b}\right)\right)= \\ \sum_{x_{b} \in Y, b \in A \backslash\{a\}} \prod_{b \in A \backslash\{a\}} p_{Y^{\{b\}}}\left(x_{b}\right) \sum_{x_{a} \in Y} p_{Y^{\{a\}}}\left(x_{a}\right)=\sum_{x_{b} \in Y, b \in A \backslash\{a\}} \prod_{b \in A \backslash\{a\}} p_{Y^{\{b\}}}\left(x_{b}\right) \end{gathered}∑xA∈YA(∏a∈ApY{a}(xa))=∑xb∈Y,b∈A∖{a}∑xa∈Y(pY{a}(xa)∏b∈A∖{a}pY{b}(xb))=∑xb∈Y,b∈A∖{a}∏b∈A∖{a}pY{b}(xb)∑xa∈YpY{a}(xa)=∑xb∈Y,b∈A∖{a}∏b∈A∖{a}pY{b}(xb)
Введя обозначение B = A ∖ { a } B = A ∖ { a } B=A\\{a}B=A \backslash\{a\}B=A∖{a}, приходим к сумме
∑ x b ∈ Y , b ∈ A ∖ { a } ∏ b ∈ A ∖ { a } p Y { b } ( x b ) = ∑ x B ∈ Y B ( ∏ b ∈ B p Y { b } ( x b ) ) , ∑ x b ∈ Y , b ∈ A ∖ { a }   ∏ b ∈ A ∖ { a }   p Y { b } x b = ∑ x B ∈ Y B   ∏ b ∈ B   p Y { b } x b , sum_(x_(b)in Y,b in A\\{a})prod_(b in A\\{a})p_(Y^({b}))(x_(b))=sum_(x_(B)inY^(B))(prod_(b in B)p_(Y^({b}))(x_(b))),\sum_{x_{b} \in Y, b \in A \backslash\{a\}} \prod_{b \in A \backslash\{a\}} p_{Y^{\{b\}}}\left(x_{b}\right)=\sum_{x_{B} \in Y^{B}}\left(\prod_{b \in B} p_{Y^{\{b\}}}\left(x_{b}\right)\right),∑xb∈Y,b∈A∖{a}∏b∈A∖{a}pY{b}(xb)=∑xB∈YB(∏b∈BpY{b}(xb)),
в которой на одно слагаемое меньше, чем в первоначальной сумме. Результатом последовательного выполнения указанных операций ( | A | − 1 | A | − 1 |A|-1|A|-1|A|−1 ) раз является равенство
∑ x A ∈ Y A p Y A ( x A ) = ∑ x a ∈ Y p Y { a } ( x a ) = 1 ∑ x A ∈ Y A   p Y A x A = ∑ x a ∈ Y   p Y { a } x a = 1 sum_(x_(A)inY^(A))p_(Y^(A))(x_(A))=sum_(x_(a)in Y)p_(Y^({a}))(x_(a))=1\sum_{x_{A} \in Y^{A}} p_{Y^{A}}\left(x_{A}\right)=\sum_{x_{a} \in Y} p_{Y^{\{a\}}}\left(x_{a}\right)=1∑xA∈YApYA(xA)=∑xa∈YpY{a}(xa)=1
означающее, что семейство P Y A = ( p Y A ( x A ) ) x A ∈ Y A P Y A = p Y A x A x A ∈ Y A P_(Y^(A))=(p_(Y^(A))(x_(A)))_(x_(A)inY^(A))P_{Y^{A}}=\left(p_{Y^{A}}\left(x_{A}\right)\right)_{x_{A} \in Y^{A}}PYA=(pYA(xA))xA∈YA действительно является распределением на Y A Y A Y^(A)Y^{A}YA.
Осталось показать, что распределения P Y A = ( p Y A ( x A ) ) x A ∈ Y A P Y A = p Y A x A x A ∈ Y A P_(Y^(A))=(p_(Y^(A))(x_(A)))_(x_(A)inY^(A))P_{Y^{A}}=\left(p_{Y^{A}}\left(x_{A}\right)\right)_{x_{A} \in Y^{A}}PYA=(pYA(xA))xA∈YA, сопоставленные всем конечным подмножествам из Z 2 Z 2 Z^(2)Z^{2}Z2, являются согласованными. Пусть A A AAA и B B BBB - непересекающиеся подмножества Z 2 Z 2 Z^(2)Z^{2}Z2. В этом случае
∑ x B ∈ Y B p Y A + B ( x A + B ) = ∑ x B ∈ Y B ( ∏ c ∈ A + B p Y { c } ( x c ) ) = ∑ x B ∈ Y B ( ∏ a ∈ A p Y { a } ( x a ) ∏ b ∈ B p Y { b } ( x b ) ) = ∏ a ∈ A p Y { a } ( x a ) ∑ x B ∈ Y B ( ∏ b ∈ B p Y { b } ( x b ) ) = = p Y A ( x A ) ∑ x B ∈ Y B p Y B ( x B ) = p Y A ( x A ) ∑ x B ∈ Y B   p Y A + B x A + B = ∑ x B ∈ Y B   ∏ c ∈ A + B   p Y { c } x c = ∑ x B ∈ Y B   ∏ a ∈ A   p Y { a } x a ∏ b ∈ B   p Y { b } x b = ∏ a ∈ A   p Y { a } x a ∑ x B ∈ Y B   ∏ b ∈ B   p Y { b } x b = = p Y A x A ∑ x B ∈ Y B   p Y B x B = p Y A x A {:[sum_(x_(B)inY^(B))p_(Y^(A+B))(x_(A+B))=sum_(x_(B)inY^(B))(prod_(c in A+B)p_(Y^({c}))(x_(c)))=],[sum_(x_(B)inY^(B))(prod_(a in A)p_(Y^({a}))(x_(a))prod_(b in B)p_(Y^({b}))(x_(b)))=prod_(a in A)p_(Y^({a}))(x_(a))sum_(x_(B)inY^(B))(prod_(b in B)p_(Y^({b}))(x_(b)))=],[=p_(Y^(A))(x_(A))sum_(x_(B)inY^(B))p_(Y^(B))(x_(B))=p_(Y^(A))(x_(A))]:}\begin{gathered} \sum_{x_{B} \in Y^{B}} p_{Y^{A+B}}\left(x_{A+B}\right)=\sum_{x_{B} \in Y^{B}}\left(\prod_{c \in A+B} p_{Y^{\{c\}}}\left(x_{c}\right)\right)= \\ \sum_{x_{B} \in Y^{B}}\left(\prod_{a \in A} p_{Y^{\{a\}}}\left(x_{a}\right) \prod_{b \in B} p_{Y^{\{b\}}}\left(x_{b}\right)\right)=\prod_{a \in A} p_{Y^{\{a\}}}\left(x_{a}\right) \sum_{x_{B} \in Y^{B}}\left(\prod_{b \in B} p_{Y^{\{b\}}}\left(x_{b}\right)\right)= \\ =p_{Y^{A}}\left(x_{A}\right) \sum_{x_{B} \in Y^{B}} p_{Y^{B}}\left(x_{B}\right)=p_{Y^{A}}\left(x_{A}\right) \end{gathered}∑xB∈YBpYA+B(xA+B)=∑xB∈YB(∏c∈A+BpY{c}(xc))=∑xB∈YB(∏a∈ApY{a}(xa)∏b∈BpY{b}(xb))=∏a∈ApY{a}(xa)∑xB∈YB(∏b∈BpY{b}(xb))==pYA(xA)∑xB∈YBpYB(xB)=pYA(xA)
Таким образом, построенное семейство конечномерных распределений является согласованным. По теореме Колмогорова существует случайное поле, для которого распределения, образующие семейство, будут конечномерными распределениями.
Следующим упрощением, вызванным теми же причинами, является предположение о том, что все случайные величины, образующие векторную случайную величину ξ A ξ A xi_(A)\xi_{A}ξA, имеют одно и тоже распределение: p Y { a } ( y ) = p A ( y ) p Y { a } ( y ) = p A ( y ) p_(Y){a}(y)=p_(A)(y)p_{Y}\{a\}(y)=p_{A}(y)pY{a}(y)=pA(y) для любых a ∈ A a ∈ A a in Aa \in Aa∈A и любых y ∈ Y y ∈ Y y in Yy \in Yy∈Y. В этом случае для любого x A = ( x a ) a ∈ A ∈ Y A x A = x a a ∈ A ∈ Y A x_(A)=(x_(a))_(a in A)inY^(A)x_{A}=\left(x_{a}\right)_{a \in A} \in Y^{A}xA=(xa)a∈A∈YA вероятность p Y A ( x A ) p Y A x A p_(Y^(A))(x_(A))p_{Y^{A}}\left(x_{A}\right)pYA(xA) принимает вид
p Y A ( x A ) = ∏ a ∈ A p Y { a } ( x a ) = ∏ a ∈ A p A ( x a ) . p Y A x A = ∏ a ∈ A   p Y { a } x a = ∏ a ∈ A   p A x a . p_(Y^(A))(x_(A))=prod_(a in A)p_(Y^({a}))(x_(a))=prod_(a in A)p_(A)(x_(a)).p_{Y^{A}}\left(x_{A}\right)=\prod_{a \in A} p_{Y^{\{a\}}}\left(x_{a}\right)=\prod_{a \in A} p_{A}\left(x_{a}\right) .pYA(xA)=∏a∈ApY{a}(xa)=∏a∈ApA(xa).
Таким образом, последнее предположение позволяет обойтись для задания конечномерного распределения P Y A = ( p Y A ( x A ) ) x A ∈ Y A P Y A = p Y A x A x A ∈ Y A P_(Y^(A))=(p_(Y^(A))(x_(A)))_(x_(A)inY^(A))P_{Y^{A}}=\left(p_{Y^{A}}\left(x_{A}\right)\right)_{x_{A} \in Y^{A}}PYA=(pYA(xA))xA∈YA только | Y | | Y | |Y||Y||Y| вероятностями распределения P A = ( p A ( y ) ) y ∈ Y P A = p A ( y ) y ∈ Y P_(A)=(p_(A)(y))_(y in Y)P_{A}=\left(p_{A}(y)\right)_{y \in Y}PA=(pA(y))y∈Y. Пример изображения случайного поля с такими свойствами приводится в конце подраздела.
Из определения построенного случайного поля следует, что образующие его случайные величины являются независимыми в совокупности и имеют одно и тоже распределение. Для случайных полей, используемых при решении прикладных задач, такое свойство является скорее исключением, а не правилом. Ниже предлагается способ построения случайного поля, между случайными величинами которого существует статистическая зависимость. Для его построения воспользуемся только что полученным результатом.
Пусть ( ζ z ) z ∈ Z 2 ζ z z ∈ Z 2 (zeta_(z))_(z inZ^(2))\left(\zeta_{z}\right)_{z \in Z^{2}}(ζz)z∈Z2 - случайное поле из независимых скалярных случай-
ных величин, имеющих одно и то же распределение со средним значением равным нулю и дисперсией σ 2 σ 2 sigma^(2)\sigma^{2}σ2. Тогда
cov ( ζ z , ζ t ) = E ζ z ζ t = { σ 2 , z = t 0 , z ≠ t cov ζ z , ζ t = E ζ z ζ t = σ 2 , z = t 0 , z ≠ t cov(zeta_(z),zeta_(t))=Ezeta_(z)zeta_(t)={[sigma^(2)","z=t],[0","z!=t]:}\operatorname{cov}\left(\zeta_{z}, \zeta_{t}\right)=E \zeta_{z} \zeta_{t}=\left\{\begin{array}{c} \sigma^{2}, z=t \\ 0, z \neq t \end{array}\right.cov(ζz,ζt)=Eζzζt={σ2,z=t0,z≠t
Квадратной окрестностью точки z ∈ Z 2 z ∈ Z 2 z inZ^(2)z \in Z^{2}z∈Z2 с радиусом r ^ r ^ hat(r)\hat{r}r^ будем называть подмножество вида
B ( z , r ^ ) = { t = ( t 1 , t 2 ) ∈ Z 2 : | z 1 − t 1 | ≤ r ^ , | z 2 − t 2 | ≤ r ^ } B ( z , r ^ ) = t = t 1 , t 2 ∈ Z 2 : z 1 − t 1 ≤ r ^ , z 2 − t 2 ≤ r ^ B(z, hat(r))={t=(t_(1),t_(2))inZ^(2):|z_(1)-t_(1)| <= ( hat(r)),|z_(2)-t_(2)| <= ( hat(r))}B(z, \hat{r})=\left\{t=\left(t_{1}, t_{2}\right) \in Z^{2}:\left|z_{1}-t_{1}\right| \leq \hat{r},\left|z_{2}-t_{2}\right| \leq \hat{r}\right\}B(z,r^)={t=(t1,t2)∈Z2:|z1−t1|≤r^,|z2−t2|≤r^}
состоящая из | B ( z , r ^ ) | = ( 2 r ^ + 1 ) 2 | B ( z , r ^ ) | = ( 2 r ^ + 1 ) 2 |B(z, hat(r))|=(2 hat(r)+1)^(2)|B(z, \hat{r})|=(2 \hat{r}+1)^{2}|B(z,r^)|=(2r^+1)2 точек. Для каждого z ∈ Z 2 z ∈ Z 2 z inZ^(2)z \in Z^{2}z∈Z2 определим случайную величину ξ z ξ z xi_(z)\xi_{z}ξz равенством
ξ z = 1 | B ( z , r ^ ) | ∑ t ∈ B ( z , r ^ ) ζ t ξ z = 1 | B ( z , r ^ ) | ∑ t ∈ B ( z , r ^ )   ζ t xi_(z)=(1)/(|B(z,( hat(r)))|)sum_(t in B(z, hat(r)))zeta_(t)\xi_{z}=\frac{1}{|B(z, \hat{r})|} \sum_{t \in B(z, \hat{r})} \zeta_{t}ξz=1|B(z,r^)|∑t∈B(z,r^)ζt
По аналогии со случайными последовательностями (см., например [63, c. 83]) назовем семейство ( ξ z ) z ∈ Z 2 ξ z z ∈ Z 2 (xi_(z))_(z inZ^(2))\left(\xi_{z}\right)_{z \in Z^{2}}(ξz)z∈Z2 случайным полем, полученным из случайного поля ( ζ z ) z ∈ Z 2 ζ z z ∈ Z 2 (zeta_(z))_(z inZ^(2))\left(\zeta_{z}\right)_{z \in Z^{2}}(ζz)z∈Z2 скользящим суммированием по окрестности B ( z , r ^ ) B ( z , r ^ ) B(z, hat(r))B(z, \hat{r})B(z,r^).
Легко подсчитать, что для каждого z ∈ Z 2 z ∈ Z 2 z inZ^(2)z \in Z^{2}z∈Z2 среднее значение E ξ z = 0 E ξ z = 0 Exi_(z)=0E \xi_{z}=0Eξz=0, дисперсия D ( ξ z ) = σ 2 / ( 2 r ^ + 1 ) 2 D ξ z = σ 2 / ( 2 r ^ + 1 ) 2 D(xi_(z))=sigma^(2)//(2 hat(r)+1)^(2)D\left(\xi_{z}\right)=\sigma^{2} /(2 \hat{r}+1)^{2}D(ξz)=σ2/(2r^+1)2, а
E ξ z ξ z + t = E ( 1 | B ( z , r ^ ) | ∑ s ∈ B ( z , r ^ ) ζ s 1 | B ( z , r ^ ) | ∑ s ∈ B ( z + t , r ^ ) ζ s ) = 1 ( 2 r ^ + 1 ) 4 ( ∑ s ∈ B ( z , r ^ ) ∑ u ∈ B ( z + t , r ^ ) E ζ s ζ u ) E ξ z ξ z + t = E 1 | B ( z , r ^ ) | ∑ s ∈ B ( z , r ^ )   ζ s 1 | B ( z , r ^ ) | ∑ s ∈ B ( z + t , r ^ )   ζ s = 1 ( 2 r ^ + 1 ) 4 ∑ s ∈ B ( z , r ^ )   ∑ u ∈ B ( z + t , r ^ )   E ζ s ζ u {:[Exi_(z)xi_(z+t)=E((1)/(|B(z,( hat(r)))|)sum_(s in B(z, hat(r)))zeta_(s)(1)/(|B(z,( hat(r)))|)sum_(s in B(z+t, hat(r)))zeta_(s))=],[(1)/((2( hat(r))+1)^(4))(sum_(s in B(z, hat(r)))sum_(u in B(z+t, hat(r)))Ezeta_(s)zeta_(u))]:}\begin{aligned} E \xi_{z} \xi_{z+t}= & E\left(\frac{1}{|B(z, \hat{r})|} \sum_{s \in B(z, \hat{r})} \zeta_{s} \frac{1}{|B(z, \hat{r})|} \sum_{s \in B(z+t, \hat{r})} \zeta_{s}\right)= \\ & \frac{1}{(2 \hat{r}+1)^{4}}\left(\sum_{s \in B(z, \hat{r})} \sum_{u \in B(z+t, \hat{r})} E \zeta_{s} \zeta_{u}\right) \end{aligned}Eξzξz+t=E(1|B(z,r^)|∑s∈B(z,r^)ζs1|B(z,r^)|∑s∈B(z+t,r^)ζs)=1(2r^+1)4(∑s∈B(z,r^)∑u∈B(z+t,r^)Eζsζu)
Если окрестности B ( z , r ^ ) B ( z , r ^ ) B(z, hat(r))B(z, \hat{r})B(z,r^) и B ( z + t , r ^ ) B ( z + t , r ^ ) B(z+t, hat(r))B(z+t, \hat{r})B(z+t,r^) не пересекаются ( | t | > 2 r ^ 2 ) ( | t | > 2 r ^ 2 ) (|t| > 2 hat(r)sqrt2)(|t|>2 \hat{r} \sqrt{2})(|t|>2r^2), то s ≠ u s ≠ u s!=us \neq us≠u. В этом случае все слагаемые в двойной сумме равны нулю. Поэтому и E ξ z ξ z + t = 0 E ξ z ξ z + t = 0 Exi_(z)xi_(z+t)=0E \xi_{z} \xi_{z+t}=0Eξzξz+t=0. В противном случае, если окрестности B ( z , r ^ ) B ( z , r ^ ) B(z, hat(r))B(z, \hat{r})B(z,r^) и B ( z + t , r ^ ) B ( z + t , r ^ ) B(z+t, hat(r))B(z+t, \hat{r})B(z+t,r^) пересекаются (это может произойти, когда 0 ≤ | t | ≤ 2 ^ r 2 0 ≤ | t | ≤ 2 ^ r 2 0 <= |t| <= widehat(2)rsqrt20 \leq|t| \leq \widehat{2} r \sqrt{2}0≤|t|≤2^r2 ), то среди всех ( 2 r ^ + 1 ) 4 ( 2 r ^ + 1 ) 4 (2 hat(r)+1)^(4)(2 \hat{r}+1)^{4}(2r^+1)4 слагаемых двойной суммы присутствуют | B ( z , r ^ ) ∩ B ( z + t , r ^ ) | | B ( z , r ^ ) ∩ B ( z + t , r ^ ) | |B(z, hat(r))nn B(z+t, hat(r))||B(z, \hat{r}) \cap B(z+t, \hat{r})||B(z,r^)∩B(z+t,r^)| слагаемых вида E ζ z ζ z = σ 2 E ζ z ζ z = σ 2 Ezeta_(z)zeta_(z)=sigma^(2)E \zeta_{z} \zeta_{z}=\sigma^{2}Eζzζz=σ2. В этом случае
cov ( ξ z , ξ z + t ) = E ξ z ξ z + t = | B ( z , r ^ ) ∩ B ( z + t , r ^ ) | ( 2 r ^ + 1 ) 4 σ 2 cov ξ z , ξ z + t = E ξ z ξ z + t = | B ( z , r ^ ) ∩ B ( z + t , r ^ ) | ( 2 r ^ + 1 ) 4 σ 2 cov(xi_(z),xi_(z+t))=Exi_(z)xi_(z+t)=(|B(z,( hat(r)))nn B(z+t,( hat(r)))|)/((2( hat(r))+1)^(4))sigma^(2)\operatorname{cov}\left(\xi_{z}, \xi_{z+t}\right)=E \xi_{z} \xi_{z+t}=\frac{|B(z, \hat{r}) \cap B(z+t, \hat{r})|}{(2 \hat{r}+1)^{4}} \sigma^{2}cov(ξz,ξz+t)=Eξzξz+t=|B(z,r^)∩B(z+t,r^)|(2r^+1)4σ2
Осталось показать, что ковариация не завит от сдвига, то есть E ξ z ξ z + t = E ξ z + a ξ z + t + a E ξ z ξ z + t = E ξ z + a ξ z + t + a Exi_(z)xi_(z+t)=Exi_(z+a)xi_(z+t+a)E \xi_{z} \xi_{z+t}=E \xi_{z+a} \xi_{z+t+a}Eξzξz+t=Eξz+aξz+t+a при любом a ∈ Z 2 a ∈ Z 2 a inZ^(2)a \in Z^{2}a∈Z2. Так как
E ξ z + a ξ z + t + a = | B ( z + a , r ^ ) ∩ B ( z + t + a , r ^ ) | ( 2 r ^ + 1 ) 4 σ 2 E ξ z + a ξ z + t + a = | B ( z + a , r ^ ) ∩ B ( z + t + a , r ^ ) | ( 2 r ^ + 1 ) 4 σ 2 Exi_(z+a)xi_(z+t+a)=(|B(z+a,( hat(r)))nn B(z+t+a,( hat(r)))|)/((2( hat(r))+1)^(4))sigma^(2)E \xi_{z+a} \xi_{z+t+a}=\frac{|B(z+a, \hat{r}) \cap B(z+t+a, \hat{r})|}{(2 \hat{r}+1)^{4}} \sigma^{2}Eξz+aξz+t+a=|B(z+a,r^)∩B(z+t+a,r^)|(2r^+1)4σ2
то осталось доказать, что
| B ( z + a , r ^ ) ∩ B ( z + t + a , r ^ ) | = | B ( z , r ^ ) ∩ B ( z + t , r ^ ) | | B ( z + a , r ^ ) ∩ B ( z + t + a , r ^ ) | = | B ( z , r ^ ) ∩ B ( z + t , r ^ ) | |B(z+a, hat(r))nn B(z+t+a, hat(r))|=|B(z, hat(r))nn B(z+t, hat(r))||B(z+a, \hat{r}) \cap B(z+t+a, \hat{r})|=|B(z, \hat{r}) \cap B(z+t, \hat{r})||B(z+a,r^)∩B(z+t+a,r^)|=|B(z,r^)∩B(z+t,r^)|
Пусть u ∈ B ( z + a , r ^ ) ∩ B ( z + t + a , r ^ ) u ∈ B ( z + a , r ^ ) ∩ B ( z + t + a , r ^ ) u in B(z+a, hat(r))nn B(z+t+a, hat(r))u \in B(z+a, \hat{r}) \cap B(z+t+a, \hat{r})u∈B(z+a,r^)∩B(z+t+a,r^), тогда должны выполняться при
j = 1 , 2 j = 1 , 2 j=1,2j=1,2j=1,2 неравенства | ( z j + t j + a j ) − u j | ≤ r ^ z j + t j + a j − u j ≤ r ^ |(z_(j)+t_(j)+a_(j))-u_(j)| <= hat(r)\left|\left(z_{j}+t_{j}+a_{j}\right)-u_{j}\right| \leq \hat{r}|(zj+tj+aj)−uj|≤r^ и | ( z j + a j ) − u j | ≤ r ^ z j + a j − u j ≤ r ^ |(z_(j)+a_(j))-u_(j)| <= hat(r)\left|\left(z_{j}+a_{j}\right)-u_{j}\right| \leq \hat{r}|(zj+aj)−uj|≤r^. Эти же неравенства после перегруппировки слагаемых | ( z j + t j ) − ( u j + a j ) | ≤ r ^ z j + t j − u j + a j ≤ r ^ |(z_(j)+t_(j))-(u_(j)+a_(j))| <= hat(r)\left|\left(z_{j}+t_{j}\right)-\left(u_{j}+a_{j}\right)\right| \leq \hat{r}|(zj+tj)−(uj+aj)|≤r^ и | ( z j ) − ( u j + a j ) | ≤ r ^ z j − u j + a j ≤ r ^ |(z_(j))-(u_(j)+a_(j))| <= hat(r)\left|\left(z_{j}\right)-\left(u_{j}+a_{j}\right)\right| \leq \hat{r}|(zj)−(uj+aj)|≤r^ означают, что ( u + a ) ∈ B ( z , r ^ ) ∩ B ( z + t , r ^ ) ( u + a ) ∈ B ( z , r ^ ) ∩ B ( z + t , r ^ ) (u+a)in B(z, hat(r))nn B(z+t, hat(r))(u+a) \in B(z, \hat{r}) \cap B(z+t, \hat{r})(u+a)∈B(z,r^)∩B(z+t,r^). Тем самым доказано включение
( B ( z + a , r ^ ) ∩ B ( z + t + a , r ^ ) ) ⊂ ( B ( z , r ^ ) ∩ B ( z + t , r ^ ) ) ( B ( z + a , r ^ ) ∩ B ( z + t + a , r ^ ) ) ⊂ ( B ( z , r ^ ) ∩ B ( z + t , r ^ ) ) (B(z+a, hat(r))nn B(z+t+a, hat(r)))sub(B(z, hat(r))nn B(z+t, hat(r)))(B(z+a, \hat{r}) \cap B(z+t+a, \hat{r})) \subset(B(z, \hat{r}) \cap B(z+t, \hat{r}))(B(z+a,r^)∩B(z+t+a,r^))⊂(B(z,r^)∩B(z+t,r^))
Обратное включение устанавливается таким же способом.
Отображение r : Z 2 × Z 2 → R r : Z 2 × Z 2 → R r:Z^(2)xxZ^(2)rarr Rr: Z^{2} \times Z^{2} \rightarrow Rr:Z2×Z2→R, определяемое равенством
r ( z , t ) = E ( ξ z − E ξ z ) ( ξ t − E ξ t ) r ( z , t ) = E ξ z − E ξ z ξ t − E ξ t r(z,t)=E(xi_(z)-Exi_(z))(xi_(t)-Exi_(t))r(z, t)=E\left(\xi_{z}-E \xi_{z}\right)\left(\xi_{t}-E \xi_{t}\right)r(z,t)=E(ξz−Eξz)(ξt−Eξt)
называется ковариационной функцией случайного поля ( ξ z ) z ∈ Z 2 ξ z z ∈ Z 2 (xi_(z))_(z inZ^(2))\left(\xi_{z}\right)_{z \in Z^{2}}(ξz)z∈Z2. Из доказанного выше следует, что для случайных полей, получаемых скользящим суммированием, выполняется равенство
r ( z , t ) = E ( ξ z − E ξ z ) ( ξ t − E ξ t ) = = E ( ξ z − t − E ξ z − t ) ( ξ 0 − E ξ 0 ) = r ( 0 , z − t ) . r ( z , t ) = E ξ z − E ξ z ξ t − E ξ t = = E ξ z − t − E ξ z − t ξ 0 − E ξ 0 = r ( 0 , z − t ) . {:[r(z","t)=E(xi_(z)-Exi_(z))(xi_(t)-Exi_(t))=],[=E(xi_(z-t)-Exi_(z-t))(xi_(0)-Exi_(0))=r(0","z-t).]:}\begin{gathered} r(z, t)=E\left(\xi_{z}-E \xi_{z}\right)\left(\xi_{t}-E \xi_{t}\right)= \\ =E\left(\xi_{z-t}-E \xi_{z-t}\right)\left(\xi_{0}-E \xi_{0}\right)=r(0, z-t) . \end{gathered}r(z,t)=E(ξz−Eξz)(ξt−Eξt)==E(ξz−t−Eξz−t)(ξ0−Eξ0)=r(0,z−t).
Оно означает, что значение r ( z , t ) r ( z , t ) r(z,t)r(z, t)r(z,t) ковариационной функции зависит только от разности ( z − t ) ( z − t ) (z-t)(z-t)(z−t). Случайные поля с такими ковариационными функциями и средними значениями, не зависящими от z ∈ Z 2 z ∈ Z 2 z inZ^(2)z \in Z^{2}z∈Z2, называются однородными в широком смысле. Их ковариационные функции являются отображениями вида r : Z 2 → R r : Z 2 → R r:Z^(2)rarr Rr: Z^{2} \rightarrow Rr:Z2→R. Поэтому значение r ( t ) r ( t ) r(t)r(t)r(t) ковариационной функции случайного поля, полученного скользящим суммирование, определя-
r ( t ) = { 0 , | t | > 2 r ^ 2 | B ( z , r ^ ) ∩ B ( z + t , r ^ ) | ( 2 r ^ + 1 ) 4 σ 2 , 0 ≤ | t | ≤ 2 r ^ 2 r ( t ) = 0 , | t | > 2 r ^ 2 | B ( z , r ^ ) ∩ B ( z + t , r ^ ) | ( 2 r ^ + 1 ) 4 σ 2 , 0 ≤ | t | ≤ 2 r ^ 2 r(t)={[0","quad|t| > 2 hat(r)sqrt2],[(|B(z,( hat(r)))nn B(z+t,( hat(r)))|)/((2( hat(r))+1)^(4))sigma^(2)","quad0 <= |t| <= 2 hat(r)sqrt2]:}r(t)=\left\{\begin{array}{c} 0, \quad|t|>2 \hat{r} \sqrt{2} \\ \frac{|B(z, \hat{r}) \cap B(z+t, \hat{r})|}{(2 \hat{r}+1)^{4}} \sigma^{2}, \quad 0 \leq|t| \leq 2 \hat{r} \sqrt{2} \end{array}\right.r(t)={0,|t|>2r^2|B(z,r^)∩B(z+t,r^)|(2r^+1)4σ2,0≤|t|≤2r^2

В таблицах 2.1 и 2.2 указаны ненулевые значения ковариационных

функций случайных полей, полученных скользящим суммированием с радиусами r ^ = 2 r ^ = 2 hat(r)=2\hat{r}=2r^=2 и r ^ = 1 r ^ = 1 hat(r)=1\hat{r}=1r^=1 соответственно. Нетрудно убедиться в том, что при r ^ = 1 r ^ = 1 hat(r)=1\hat{r}=1r^=1 ковариационная функция зависит только от расстояния | t − z | | t − z | |t-z||t-z||t−z| между случайными величинами ξ t ξ t xi_(t)\xi_{t}ξt и ξ z ξ z xi_(z)\xi_{z}ξz. Случайны поля с такими функциями называются однородными и изотропными.
Таблица 2.1 - Ковариационная функция ( r ^ = 2 r ^ = 2 hat(r)=2\hat{r}=2r^=2 )
Координата t 2 t 2 t_(2)t_{2}t2 Координата t 1 t 1 t_(1)t_{1}t1
0 1 2 3 4 ≥ 5 ≥ 5 >= 5\geq 5≥5
0 1.00 0.80 0.60 0.40 0.20 0
1 0.80 0.64 0.48 0.32 0.16 0
2 0.60 0.48 0.36 0.24 0.12 0
3 0.40 0.32 0.24 0.20 0.08 0
4 0.20 0.16 0.12 0.08 0.04 0
≥ 5 ≥ 5 >= 5\geq 5≥5 0 0 0 0 0 0
Координата t_(2) Координата t_(1) 0 1 2 3 4 >= 5 0 1.00 0.80 0.60 0.40 0.20 0 1 0.80 0.64 0.48 0.32 0.16 0 2 0.60 0.48 0.36 0.24 0.12 0 3 0.40 0.32 0.24 0.20 0.08 0 4 0.20 0.16 0.12 0.08 0.04 0 >= 5 0 0 0 0 0 0| Координата $t_{2}$ | Координата $t_{1}$ | | | | | | | :--- | :--- | :--- | :--- | :--- | :--- | :--- | | | 0 | 1 | 2 | 3 | 4 | $\geq 5$ | | 0 | 1.00 | 0.80 | 0.60 | 0.40 | 0.20 | 0 | | 1 | 0.80 | 0.64 | 0.48 | 0.32 | 0.16 | 0 | | 2 | 0.60 | 0.48 | 0.36 | 0.24 | 0.12 | 0 | | 3 | 0.40 | 0.32 | 0.24 | 0.20 | 0.08 | 0 | | 4 | 0.20 | 0.16 | 0.12 | 0.08 | 0.04 | 0 | | $\geq 5$ | 0 | 0 | 0 | 0 | 0 | 0 |
Таблица 2.2 - Ковариационная функция ( r ^ = 1 r ^ = 1 hat(r)=1\hat{r}=1r^=1 )
Координата t 2 t 2 t_(2)t_{2}t2 Координата t 1 t 1 t_(1)t_{1}t1
0 1 2 ≥ 3 ≥ 3 >= 3\geq 3≥3
0 1.00 0.67 0.33 0
1 0.67 0.44 0.22 0
2 0.33 0.22 0.11 0
3 0 0 0 0
Координата t_(2) Координата t_(1) 0 1 2 >= 3 0 1.00 0.67 0.33 0 1 0.67 0.44 0.22 0 2 0.33 0.22 0.11 0 3 0 0 0 0| Координата $t_{2}$ | Координата $t_{1}$ | | | | | :--- | :--- | :--- | :--- | :--- | | | 0 | 1 | 2 | $\geq 3$ | | 0 | 1.00 | 0.67 | 0.33 | 0 | | 1 | 0.67 | 0.44 | 0.22 | 0 | | 2 | 0.33 | 0.22 | 0.11 | 0 | | 3 | 0 | 0 | 0 | 0 |
Ниже приведены квадратные фрагменты со стороной 256 пикселей изображений трех случайных полей, полученные с помощью компьютера. Изображение с рисунка 1.5.1 соответствует случайному полю из независимых в совокупности случайных величин, имеющим нормальное распределение со средним значением m = 128 m = 128 m=128m=128m=128 и СКО σ = 30 σ = 30 sigma=30\sigma=30σ=30. В таблице 2.3 приведены оценки значений нормированной ковариационной функции, вычисленные по этому изображению. Они хорошо согласуются с теоретическими значениями.
Таблица 2.3 - Оценка ковариационной функции ( r ^ = 0 r ^ = 0 hat(r)=0\hat{r}=0r^=0 )
Коор- Координата t 1 t 1 t_(1)t_{1}t1
дината 0 1 2 3 4 5
t 2 t 2 t_(2)t_{2}t2
0 1.00 -0.01 0.01 0.00 0.01 0.00
Коор- Координата t_(1) дината 0 1 2 3 4 5 t_(2) 0 1.00 -0.01 0.01 0.00 0.01 0.00 | Коор- | Координата $t_{1}$ | | | | | | | | :---: | ---: | ---: | ---: | ---: | ---: | ---: | :---: | | дината | 0 | 1 | 2 | 3 | 4 | 5 | | | $t_{2}$ | | | | | | | | | 0 | 1.00 | -0.01 | 0.01 | 0.00 | 0.01 | 0.00 | |
1 0.00 0.00 0.01 0.01 0.00 0.01
0.00 0.00 0.01 0.01 0.01 0.00
2 0.00 0.00 0.01 0.00 0.00 -
3 0.01
0.00 0.01 0.01 0.01 0.02 0.00
4 0.00 0.00 0.00 0.01 0.00 0.00
5
1 0.00 0.00 0.01 0.01 0.00 0.01 0.00 0.00 0.01 0.01 0.01 0.00 2 0.00 0.00 0.01 0.00 0.00 - 3 0.01 0.00 0.01 0.01 0.01 0.02 0.00 4 0.00 0.00 0.00 0.01 0.00 0.00 5 | 1 | 0.00 | 0.00 | 0.01 | 0.01 | 0.00 | 0.01 | | :--- | :--- | :--- | :--- | :--- | :--- | :--- | | | 0.00 | 0.00 | 0.01 | 0.01 | 0.01 | 0.00 | | 2 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | - | | 3 | 0.01 | | | | | | | | 0.00 | 0.01 | 0.01 | 0.01 | 0.02 | 0.00 | | 4 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | | 5 | | | | | | |
На рисунках 1.5.2 и 1.5.3 приведены изображения случайных полей, полученных скользящим суммированием по окрестностям B ( z , r ^ ) B ( z , r ^ ) B(z, hat(r))B(z, \hat{r})B(z,r^) с радиусами r ^ = 1 r ^ = 1 hat(r)=1\hat{r}=1r^=1 и r ^ = 2 r ^ = 2 hat(r)=2\hat{r}=2r^=2 соответственно из случайного поля из независимых в совокупности случайных величин. Оценки средних значений, вычисленные по изображениям этих полей, совпали со средним значением исходного случайного поля. Оценки СКО равны 10 и 6 уровням, что совпало с теоретическими значениями. В таблицах 2.4 и 2.5 приведены оценки значений нормированных ковариационных функций, вычисленные по соответствующим изображениям...
Рисунок 1.5.1 - Изображение случайного поля с попарно независимыми случайными величинами
Рисунок 1.5.2 - Изображение случайного поля, полученного скользящим
( r ^ = 1 r ^ = 1 hat(r)=1\hat{r}=1r^=1 )
Рисунок 1.5.3 - Изображение случайного поля, полученного скользящим ( r ^ = 2 r ^ = 2 hat(r)=2\hat{r}=2r^=2 )
Таблица 2.4 - Оценка ковариационной функции ( r = 1 r = 1 r=1r=1r=1 )
Координата t 2 t 2 t_(2)t_{2}t2 Координата t 1 t 1 t_(1)t_{1}t1
0 1 2 3 4
0 1.00 0.67 0.33 -0.01 -0.01 -
1 0.02
2 0.66 0.44 0.22 -0.02 -0.03
3
4 0.03
5 0.03
0.02 0.02 0.02 0.00 -0.01 -
0.03 0.04 0.040 .02 0.00 0.01
0.01
Координата t_(2) Координата t_(1) 0 1 2 3 4 0 1.00 0.67 0.33 -0.01 -0.01 - 1 0.02 2 0.66 0.44 0.22 -0.02 -0.03 3 4 0.03 5 0.03 0.02 0.02 0.02 0.00 -0.01 - 0.03 0.04 0.040 .02 0.00 0.01 0.01 | Координата $t_{2}$ | Координата $t_{1}$ | | | | | | :--- | :--- | :--- | :--- | :--- | :--- | | | 0 | 1 | 2 | 3 | 4 | | 0 | 1.00 | 0.67 | 0.33 | -0.01 | -0.01 - | | 1 | 0.02 | | | | | | 2 | 0.66 | 0.44 | 0.22 | -0.02 | -0.03 | | 3 | | | | | | | 4 | 0.03 | | | | | | 5 | 0.03 | | | | | | | 0.02 | 0.02 | 0.02 | 0.00 | -0.01 - | | | 0.03 | 0.04 | | 0.040 .02 0.00 | 0.01 | | | 0.01 | | | | |
Таблица 2.4 - Оценка ковариационной функции ( r = 2 r = 2 r=2r=2r=2 )
Координата t 2 t 2 t_(2)t_{2}t2 Координата t 1 t 1 t_(1)t_{1}t1
0 1 2 3 5
0 1.00 0.82 0.63 0.44 0.24
1 0.03
2
0.82
0.05
0.05
0.63
0.82 0.05 0.05 0.63| 0.82 | | :--- | | 0.05 | | 0.05 | | 0.63 |
 0.68 0.53 0.38 0.22
3
4
5 0.06
0.04
0.22 0.21 0.16 0.14 0.08
0.03
0.00 0.03 0.03 0.04 0.03
0.01
Координата t_(2) Координата t_(1) 0 1 2 3 5 0 1.00 0.82 0.63 0.44 0.24 1 0.03 2 "0.82 0.05 0.05 0.63" 0.68 0.53 0.38 0.22 3 4 5 0.06 0.04 0.22 0.21 0.16 0.14 0.08 0.03 0.00 0.03 0.03 0.04 0.03 0.01 | Координата $t_{2}$ | Координата $t_{1}$ | | | | | | :--- | :--- | :--- | :--- | :--- | :--- | | | 0 | 1 | 2 | 3 | 5 | | 0 | 1.00 | 0.82 | 0.63 | 0.44 | 0.24 | | 1 | 0.03 | | | | | | 2 | 0.82 <br> 0.05 <br> 0.05 <br> 0.63 | 0.68 | 0.53 | 0.38 | 0.22 | | 3 | | | | | | | | | 4 | | | | | | | | | | | | | | | 5 | 0.06 | | | | | | | 0.04 | | | | | | | 0.22 | 0.21 | 0.16 | | 0.14 | 0.08 | | | 0.03 | | | | | | | 0.00 | 0.03 | 0.03 | 0.04 | 0.03 | | | 0.01 | | | | |

1.7 Однородные случайные поля

Ковариационная функция. Характеристическое свойство ковариационной функции. Определение однородного случайного поля и свойства его ковариационной функции.
Если задано случайное поле ( ξ z ) z ∈ Z 2 ξ z z ∈ Z 2 (xi_(z))_(z inZ^(2))\left(\xi_{z}\right)_{z \in Z^{2}}(ξz)z∈Z2, то каждой паре z z zzz и t t ttt из Z 2 Z 2 Z^(2)Z^{2}Z2 можно поставить в соответствие ковариацию cov ( ξ z , ξ t ) = E ( ξ z − E ξ z ) ( ξ t − E ξ t ) cov ξ z , ξ t = E ξ z − E ξ z ξ t − E ξ t cov(xi_(z),xi_(t))=E(xi_(z)-Exi_(z))(xi_(t)-Exi_(t))\operatorname{cov}\left(\xi_{z}, \xi_{t}\right)=E\left(\xi_{z}-E \xi_{z}\right)\left(\xi_{t}-E \xi_{t}\right)cov(ξz,ξt)=E(ξz−Eξz)(ξt−Eξt) случайных величин ξ z ξ z xi_(z)\xi_{z}ξz и ξ t ξ t xi_(t)\xi_{t}ξt. Отображение r : Z 2 → R r : Z 2 → R r:Z^(2)rarr Rr: Z^{2} \rightarrow Rr:Z2→R, определяемое равенством r ( z , t ) = cov ( ξ z , ξ t ) r ( z , t ) = cov ξ z , ξ t r(z,t)=cov(xi_(z),xi_(t))r(z, t)=\operatorname{cov}\left(\xi_{z}, \xi_{t}\right)r(z,t)=cov(ξz,ξt), называется ковариационной функцией случайного поля.
(1.7.1) Пусть n n nnn - натуральное число, c j , 1 ≤ j ≤ n c j , 1 ≤ j ≤ n c_(j),1 <= j <= nc_{j}, 1 \leq j \leq ncj,1≤j≤n, - произвольные вещественные числа, среди которых не все нули, тогда имеет место неравенство
∑ 1 ≤ j , i ≤ n r ( z j , t i ) c j c i ≥ 0 ∑ 1 ≤ j , i ≤ n   r z j , t i c j c i ≥ 0 sum_(1 <= j,i <= n)r(z_(j),t_(i))c_(j)c_(i) >= 0\sum_{1 \leq j, i \leq n} r\left(z_{j}, t_{i}\right) c_{j} c_{i} \geq 0∑1≤j,i≤nr(zj,ti)cjci≥0
Доказательство. В самом деле
∑ 1 ≤ j , i ≤ n r ( z i , t j ) c z i c t j = ∑ i = 1 n ∑ j = 1 n cov ( ξ z i , ξ t j ) c z i c t j = E ( ∑ i = 1 n ∑ j = 1 n c z i ( ξ z i − m z i ) c t j ( ξ t j − m t j ) ) = E ( ∑ i = 1 n c z i ( ξ z i − m z i ) ) 2 ≥ 0 ∑ 1 ≤ j , i ≤ n   r z i , t j c z i c t j = ∑ i = 1 n   ∑ j = 1 n   cov ξ z i , ξ t j c z i c t j = E ∑ i = 1 n   ∑ j = 1 n   c z i ξ z i − m z i c t j ξ t j − m t j = E ∑ i = 1 n   c z i ξ z i − m z i 2 ≥ 0 {:[sum_(1 <= j,i <= n)r(z_(i),t_(j))c_(z_(i))c_(t_(j))=sum_(i=1)^(n)sum_(j=1)^(n)cov(xi_(z_(i)),xi_(t_(j)))c_(z_(i))c_(t_(j))=],[E(sum_(i=1)^(n)sum_(j=1)^(n)c_(z_(i))(xi_(z_(i))-m_(z_(i)))c_(t_(j))(xi_(t_(j))-m_(t_(j))))=E(sum_(i=1)^(n)c_(z_(i))(xi_(z_(i))-m_(z_(i))))^(2) >= 0]:}\begin{gathered} \sum_{1 \leq j, i \leq n} r\left(z_{i}, t_{j}\right) c_{z_{i}} c_{t_{j}}=\sum_{i=1}^{n} \sum_{j=1}^{n} \operatorname{cov}\left(\xi_{z_{i}}, \xi_{t_{j}}\right) c_{z_{i}} c_{t_{j}}= \\ E\left(\sum_{i=1}^{n} \sum_{j=1}^{n} c_{z_{i}}\left(\xi_{z_{i}}-m_{z_{i}}\right) c_{t_{j}}\left(\xi_{t_{j}}-m_{t_{j}}\right)\right)=E\left(\sum_{i=1}^{n} c_{z_{i}}\left(\xi_{z_{i}}-m_{z_{i}}\right)\right)^{2} \geq 0 \end{gathered}∑1≤j,i≤nr(zi,tj)czictj=∑i=1n∑j=1ncov(ξzi,ξtj)czictj=E(∑i=1n∑j=1nczi(ξzi−mzi)ctj(ξtj−mtj))=E(∑i=1nczi(ξzi−mzi))2≥0
Функции от двух переменных вида f : Z × Z → R f : Z × Z → R f:Z xx Z rarr Rf: Z \times Z \rightarrow Rf:Z×Z→R, для которых выполняется неравенство
∑ 1 ≤ j , i ≤ n f ( z j , t i ) c j c i ≥ 0 ∑ 1 ≤ j , i ≤ n   f z j , t i c j c i ≥ 0 sum_(1 <= j,i <= n)f(z_(j),t_(i))c_(j)c_(i) >= 0\sum_{1 \leq j, i \leq n} f\left(z_{j}, t_{i}\right) c_{j} c_{i} \geq 0∑1≤j,i≤nf(zj,ti)cjci≥0
при любых вещественных c j , 1 ≤ j ≤ n c j , 1 ≤ j ≤ n c_(j),1 <= j <= nc_{j}, 1 \leq j \leq ncj,1≤j≤n, и любых z j , t i z j , t i z_(j),t_(i)z_{j}, t_{i}zj,ti из Z 2 Z 2 Z^(2)Z^{2}Z2, называются неотрицательно определенными. Из доказанной теоремы следует, что каждая ковариационная функция является таковой. Следующая теорема утверждает, что верно и обратное утверждение.
(1.7.2) Если f f fff - неотрицательно определенная на Z 2 Z 2 Z^(2)Z^{2}Z2 функция, то существует случайное поле ( ξ z ) z ∈ Z 2 ξ z z ∈ Z 2 (xi_(z))_(z inZ^(2))\left(\xi_{z}\right)_{z \in Z^{2}}(ξz)z∈Z2 со средним значением m z = 0 , z ∈ Z 2 m z = 0 , z ∈ Z 2 m_(z)=0,z inZ^(2)m_{z}=0, z \in Z^{2}mz=0,z∈Z2, для которого f f fff является ковариационной функцией
E ξ z ξ t = f ( ξ z , ξ t ) , z ∈ Z 2 , t ∈ Z 2 . E ξ z ξ t = f ξ z , ξ t , z ∈ Z 2 , t ∈ Z 2 . Exi_(z)xi_(t)=f(xi_(z),xi_(t)),z inZ^(2),t inZ^(2).E \xi_{z} \xi_{t}=f\left(\xi_{z}, \xi_{t}\right), z \in Z^{2}, t \in Z^{2} .Eξzξt=f(ξz,ξt),z∈Z2,t∈Z2.
С доказательством теоремы можно ознакомиться по работам [XX]. А здесь намечены его основные этапы. Ранее в 1.4 показано, что нормальное распределение n n nnn-мерной случайной величины ξ = ( ξ j ) 1 ≤ j ≤ n ξ = ξ j 1 ≤ j ≤ n xi=(xi_(j))_(1 <= j <= n)\xi=\left(\xi_{j}\right)_{1 \leq j \leq n}ξ=(ξj)1≤j≤n однозначно определяется вектором средних значений m = ( m j ) 1 ≤ j ≤ n , m j = E ξ j m = m j 1 ≤ j ≤ n , m j = E ξ j m=(m_(j))_(1 <= j <= n),m_(j)=Exi_(j)m=\left(m_{j}\right)_{1 \leq j \leq n}, m_{j}=E \xi_{j}m=(mj)1≤j≤n,mj=Eξj и ковариационной матрицей C = ( c i j ) 1 ≤ i , j ≤ n , c i j = cov ( ξ i , ξ j ) C = c i j 1 ≤ i , j ≤ n , c i j = cov ξ i , ξ j C=(c_(ij))_(1 <= i,j <= n),c_(ij)=cov(xi_(i),xi_(j))C=\left(c_{i j}\right)_{1 \leq i, j \leq n}, c_{i j}=\operatorname{cov}\left(\xi_{i}, \xi_{j}\right)C=(cij)1≤i,j≤n,cij=cov(ξi,ξj), которая является неотрицательно определенной. Пусть r r rrr - неотрицательно определенная функция на Z 2 Z 2 Z^(2)Z^{2}Z2. Каждому конечному подмножеству A ⊂ Z 2 A ⊂ Z 2 A subZ^(2)A \subset Z^{2}A⊂Z2 можно сопоставить, используя r r rrr, неотрицательно определенную ковариационную матрицу r ( z , t ) = cov ( ξ z , ξ t ) r ( z , t ) = cov ξ z , ξ t r(z,t)=cov(xi_(z),xi_(t))r(z, t)=\operatorname{cov}\left(\xi_{z}, \xi_{t}\right)r(z,t)=cov(ξz,ξt), z , t ∈ A z , t ∈ A z,t in Az, t \in Az,t∈A. Она задает | A | | A | |A||\mathrm{A}||A| - мерное нормальное распределение векторной случайной величины ( ξ a ) a ∈ A ξ a a ∈ A (xi_(a))_(a in A)\left(\xi_{a}\right)_{a \in A}(ξa)a∈A. Доказывается, что семейство таких распределений является согласованным. В соответствии с теоремой Колмогорова оно задает на Z 2 Z 2 Z^(2)Z^{2}Z2 случайное поле, ковариационной функцией которого является r r rrr.
Случайная величина считается заданной, если известно ее распределение вероятностей. Однако важная информация о случайной величине содержится в ее числовых характеристиках, главными из которых являются среднее значение и дисперсия. Если для решения поставленной задачи достаточно только этой информации, то можно использовать любую случайную величину с заданными средним значением и дисперсией. При этом следует помнить, что для задания случайной величины этих сведений недостаточно. Оказывается, что похожим образом обстоят дела и в случае случайных полей. При решении широкого класса прикладных задач оказывается достаточно знать только среднее значение ( m z ) z ∈ Z 2 m z z ∈ Z 2 (m_(z))_(z inZ^(2))\left(m_{z}\right)_{z \in Z^{2}}(mz)z∈Z2 и ковариационную функцию r r rrr случайного поля. Поэтому для его задания вместо семейства согласованных конечномерных распределений, можно использовать неотрицательно определенную функцию с нужными свойствами. Теорема (1.7.2) утверждает, что всегда существует случайное поле, для которого она является ковариационной функцией.
Довольно часто предполагается, что свойства случайного поля, описываемые средним значением и ковариационной функцией, должны оставаться неизменными для различных z ∈ Z 2 z ∈ Z 2 z inZ^(2)z \in Z^{2}z∈Z2. Формально это приводит к требованиям о том, что среднее значение m z m z m_(z)m_{z}mz поля должно быть константой: m z = m , z ∈ Z 2 m z = m , z ∈ Z 2 m_(z)=m,z inZ^(2)m_{z}=m, z \in Z^{2}mz=m,z∈Z2, а значение ковариационной функции не должно изменяться при сдвиге на произвольный вектор a ∈ Z 2 a ∈ Z 2 a inZ^(2)a \in Z^{2}a∈Z2
r ( ξ z + a , ξ t + a ) = r ( ξ z , ξ t ) = r ( ξ z − t , ξ 0 ) . r ξ z + a , ξ t + a = r ξ z , ξ t = r ξ z − t , ξ 0 . r(xi_(z+a),xi_(t+a))=r(xi_(z),xi_(t))=r(xi_(z-t),xi_(0)).r\left(\xi_{z+a}, \xi_{t+a}\right)=r\left(\xi_{z}, \xi_{t}\right)=r\left(\xi_{z-t}, \xi_{0}\right) .r(ξz+a,ξt+a)=r(ξz,ξt)=r(ξz−t,ξ0).
Случайные поля, удовлетворяющие этому предположению, называются однородными случайными полями в широком смысле. Поскольку далее будут рассматриваться только такие случайные поля, то слова «в широком смысле» будут, как правило, опускаться. Так как значение r ( ξ z , ξ t ) r ξ z , ξ t r(xi_(z),xi_(t))r\left(\xi_{z}, \xi_{t}\right)r(ξz,ξt) ковариационной функции однородного случайного поля зависит только от разности z − t z − t z-tz-tz−t, то далее ковариация случайных величин ξ z ξ z xi_(z)\xi_{z}ξz и ξ t ξ t xi_(t)\xi_{t}ξt однородного случайного поля будет обозначаться cov ( ξ z + t , ξ z ) = r ( t ) cov ξ z + t , ξ z = r ( t ) cov(xi_(z+t),xi_(z))=r(t)\operatorname{cov}\left(\xi_{z+t}, \xi_{z}\right)=r(t)cov(ξz+t,ξz)=r(t).
Сделанные предположения позволяют установить следующие свойства ковариационной функции однородного случайного поля
r ( 0 ) ≥ 0 , r ( t ) = r ( − t ) , | r ( t ) | ≤ r ( 0 ) r ( 0 ) ≥ 0 , r ( t ) = r ( − t ) , | r ( t ) | ≤ r ( 0 ) r(0) >= 0,quad r(t)=r(-t),quad|r(t)| <= r(0)r(0) \geq 0, \quad r(t)=r(-t), \quad|r(t)| \leq r(0)r(0)≥0,r(t)=r(−t),|r(t)|≤r(0)
Из определения следует, что
r ( 0 ) = cov ( ξ z + 0 , ξ z ) = E ( ξ z − m ) 2 = D ξ z ≥ 0 r ( 0 ) = cov ξ z + 0 , ξ z = E ξ z − m 2 = D ξ z ≥ 0 r(0)=cov(xi_(z+0),xi_(z))=E(xi_(z)-m)^(2)=Dxi_(z) >= 0r(0)=\operatorname{cov}\left(\xi_{z+0}, \xi_{z}\right)=E\left(\xi_{z}-m\right)^{2}=D \xi_{z} \geq 0r(0)=cov(ξz+0,ξz)=E(ξz−m)2=Dξz≥0
Строгое неравенство r ( 0 ) > 0 r ( 0 ) > 0 r(0) > 0r(0)>0r(0)>0 имеет место только в том случае, когда ξ z ξ z xi_(z)\xi_{z}ξz не является константой. Второе свойство следует также из определения
r ( t ) = E ( ξ z + t − m ) ( ξ z − m ) = E ( ξ z − m ) ( ξ z + t − m ) = r ( − t ) . r ( t ) = E ξ z + t − m ξ z − m = E ξ z − m ξ z + t − m = r ( − t ) . r(t)=E(xi_(z+t)-m)(xi_(z)-m)=E(xi_(z)-m)(xi_(z+t)-m)=r(-t).r(t)=E\left(\xi_{z+t}-m\right)\left(\xi_{z}-m\right)=E\left(\xi_{z}-m\right)\left(\xi_{z+t}-m\right)=r(-t) .r(t)=E(ξz+t−m)(ξz−m)=E(ξz−m)(ξz+t−m)=r(−t).
Для доказательства третьего свойства воспользуемся неравенством | E ξ η | ≤ E | ξ η | | E ξ η | ≤ E | ξ η | |E xi eta| <= E|xi eta||E \xi \eta| \leq E|\xi \eta||Eξη|≤E|ξη| и неравенством Буняковского-Коши-Шварца E | ξ η | ≤ E ( ξ ) 2 E ( η ) 2 E | ξ η | ≤ E ( ξ ) 2 E ( η ) 2 E|xi eta| <= sqrt(E(xi)^(2)E(eta)^(2))E|\xi \eta| \leq \sqrt{E(\xi)^{2} E(\eta)^{2}}E|ξη|≤E(ξ)2E(η)2, доказательство которого приводится в 1.2.
| r ( t ) | = | E ( ξ z − m ) ( ξ z + t − m ) | ≤ E | ( ξ z − m ) ( ξ z + t − m ) | ≤ ≤ ( E ( ξ z − m ) 2 E ( ξ z + t − m ) 2 ) 1 2 = r ( 0 ) | r ( t ) | = E ξ z − m ξ z + t − m ≤ E ξ z − m ξ z + t − m ≤ ≤ E ξ z − m 2 E ξ z + t − m 2 1 2 = r ( 0 ) {:[|r(t)|=|E(xi_(z)-m)(xi_(z+t)-m)| <= E|(xi_(z)-m)(xi_(z+t)-m)| <= ],[ <= (E(xi_(z)-m)^(2)E(xi_(z+t)-m)^(2))^((1)/(2))=r(0)]:}\begin{gathered} |r(t)|=\left|E\left(\xi_{z}-m\right)\left(\xi_{z+t}-m\right)\right| \leq E\left|\left(\xi_{z}-m\right)\left(\xi_{z+t}-m\right)\right| \leq \\ \leq\left(E\left(\xi_{z}-m\right)^{2} E\left(\xi_{z+t}-m\right)^{2}\right)^{\frac{1}{2}}=r(0) \end{gathered}|r(t)|=|E(ξz−m)(ξz+t−m)|≤E|(ξz−m)(ξz+t−m)|≤≤(E(ξz−m)2E(ξz+t−m)2)12=r(0)

1.8 Теорема Слуцкого

Довольно часто при решении прикладных задач доступная информация об однородном случайном поле представлена набором его выборочных поверхностей. Ниже формулируется теорема, принадлежащая Слуцкому Е. Е. Она определяет условия, при выполнении которых среднее арифметическое значение, вычисленное по ограниченному фрагменту единственной выборочной поверхности, может использоваться в качестве оценки неизвестного среднего значения. Теорема была доказана Слуцким для стационарных в широком смысле случайных процессов. Предлагаемая ниже теорема (1.7.1) является ее естественным обобщением для случая, когда семейство случайных величин является однородным случайным полем.
Последовательность ( ξ n ) n ≥ 1 ξ n n ≥ 1 (xi_(n))_(n >= 1)\left(\xi_{n}\right)_{n \geq 1}(ξn)n≥1 случайных величин называется сходящейся к случайной величине ξ ξ xi\xiξ в среднеквадратическом, если числовая последовательность E ( ξ n − ξ ) 2 E ξ n − ξ 2 E(xi_(n)-xi)^(2)E\left(\xi_{n}-\xi\right)^{2}E(ξn−ξ)2 из средних значений сходится к нулю:
lim n → + ∞ E ( ξ n − ξ ) 2 = 0 lim n → + ∞   E ξ n − ξ 2 = 0 lim_(n rarr+oo)E(xi_(n)-xi)^(2)=0\lim _{n \rightarrow+\infty} E\left(\xi_{n}-\xi\right)^{2}=0limn→+∞E(ξn−ξ)2=0
Далее такая сходимость будет обозначаться ξ n → ξ ξ n → ξ xi_(n)rarr xi\xi_{n} \rightarrow \xiξn→ξ в ср. кв.
Последовательность ( ξ n ) n ≥ 1 ξ n n ≥ 1 (xi_(n))_(n >= 1)\left(\xi_{n}\right)_{n \geq 1}(ξn)n≥1 случайных величин называется сходящейся к случайной величине ξ ξ xi\xiξ по вероятности, если для любого ε > 0 ε > 0 epsi > 0\varepsilon>0ε>0 числовая последовательность P ( | ξ n − ξ | ≤ ε ) P ξ n − ξ ≤ ε P(|xi_(n)-xi| <= epsi)P\left(\left|\xi_{n}-\xi\right| \leq \varepsilon\right)P(|ξn−ξ|≤ε) сходится к нулю
lim n → + ∞ P ( | ξ n − ξ | > ε ) = 0 lim n → + ∞   P ξ n − ξ > ε = 0 lim_(n rarr+oo)P(|xi_(n)-xi| > epsi)=0\lim _{n \rightarrow+\infty} P\left(\left|\xi_{n}-\xi\right|>\varepsilon\right)=0limn→+∞P(|ξn−ξ|>ε)=0
Такая сходимость ( ξ n ) n ≥ 1 ξ n n ≥ 1 (xi_(n))_(n >= 1)\left(\xi_{n}\right)_{n \geq 1}(ξn)n≥1 к ξ ξ xi\xiξ будет обозначаться ξ n → P ξ ξ n → P ξ xi_(n)rarr"P"xi\xi_{n} \xrightarrow{P} \xiξn→Pξ.
Легко показать, что из сходимости ξ n → ξ ξ n → ξ xi_(n)rarr xi\xi_{n} \rightarrow \xiξn→ξ в ср. кв. следует сходимость ξ n → P ξ ξ n → P ξ xi_(n)rarr"P"xi\xi_{n} \xrightarrow{P} \xiξn→Pξ по вероятности. В самом деле, применяя неравенство Чебышева к разности ξ n − ξ ξ n − ξ xi_(n)-xi\xi_{n}-\xiξn−ξ, получаем для любого ε > 0 ε > 0 epsi > 0\varepsilon>0ε>0 неравенство
P ( | ξ n − ξ | > ε ) ≤ E ( ξ n − ξ ) 2 ε 2 . P ξ n − ξ > ε ≤ E ξ n − ξ 2 ε 2 . P(|xi_(n)-xi| > epsi) <= (E(xi_(n)-xi)^(2))/(epsi^(2)).P\left(\left|\xi_{n}-\xi\right|>\varepsilon\right) \leq \frac{E\left(\xi_{n}-\xi\right)^{2}}{\varepsilon^{2}} .P(|ξn−ξ|>ε)≤E(ξn−ξ)2ε2.
Из сходимости ξ n → ξ ξ n → ξ xi_(n)rarr xi\xi_{n} \rightarrow \xiξn→ξ в ср. кв. следует, что lim n → + ∞ E ( ξ n − ξ ) 2 = 0 lim n → + ∞   E ξ n − ξ 2 = 0 lim_(n rarr+oo)E(xi_(n)-xi)^(2)=0\lim _{n \rightarrow+\infty} E\left(\xi_{n}-\xi\right)^{2}=0limn→+∞E(ξn−ξ)2=0. Поэтому для любых δ > 0 δ > 0 delta > 0\delta>0δ>0 и ε > 0 ε > 0 epsi > 0\varepsilon>0ε>0 существует такое n ( δ , ε ) n ( δ , ε ) n(delta,epsi)n(\delta, \varepsilon)n(δ,ε), что E ( ξ n − ξ ) 2 < δ ε 2 E ξ n − ξ 2 < δ ε 2 E(xi_(n)-xi)^(2) < deltaepsi^(2)E\left(\xi_{n}-\xi\right)^{2}<\delta \varepsilon^{2}E(ξn−ξ)2<δε2 при n > n ( δ , ε ) , a n > n ( δ , ε ) , a n > n(delta,epsi),an> n(\delta, \varepsilon), \mathrm{a}n>n(δ,ε),a
P ( | ξ n − ξ | > ε ) < δ . P ξ n − ξ > ε < δ . P(|xi_(n)-xi| > epsi) < delta.P\left(\left|\xi_{n}-\xi\right|>\varepsilon\right)<\delta .P(|ξn−ξ|>ε)<δ.
Это означает, что ( ξ n ) n ≥ 1 ξ n n ≥ 1 (xi_(n))_(n >= 1)\left(\xi_{n}\right)_{n \geq 1}(ξn)n≥1 сходится к ξ ξ xi\xiξ по вероятности. Отметим, что обратное утверждение неверно: из сходимости по вероятности не следует сходимость в ср. кв.
После замены события | ξ n − ξ | > ε ξ n − ξ > ε |xi_(n)-xi| > epsi\left|\xi_{n}-\xi\right|>\varepsilon|ξn−ξ|>ε из левой части последнего неравенства на противоположное | ξ n − ξ | ≤ ε ξ n − ξ ≤ ε |xi_(n)-xi| <= epsi\left|\xi_{n}-\xi\right| \leq \varepsilon|ξn−ξ|≤ε следует неравенство
P ( | ξ n − ξ | ≤ ε ) = 1 − P ( | ξ n − ξ | > ε ) > 1 − δ , P ξ n − ξ ≤ ε = 1 − P ξ n − ξ > ε > 1 − δ , P(|xi_(n)-xi| <= epsi)=1-P(|xi_(n)-xi| > epsi) > 1-delta,P\left(\left|\xi_{n}-\xi\right| \leq \varepsilon\right)=1-P\left(\left|\xi_{n}-\xi\right|>\varepsilon\right)>1-\delta,P(|ξn−ξ|≤ε)=1−P(|ξn−ξ|>ε)>1−δ,
которое выполняется при любых n > n ( δ , ε ) n > n ( δ , ε ) n > n(delta,epsi)n>n(\delta, \varepsilon)n>n(δ,ε). Поэтому, если ω ∈ Ω , x = ξ ( ω ) ω ∈ Ω , x = ξ ( ω ) omega in Omega,x=xi(omega)\omega \in \Omega, x=\xi(\omega)ω∈Ω,x=ξ(ω) и x n = ξ n ( ω ) x n = ξ n ( ω ) x_(n)=xi_(n)(omega)x_{n}=\xi_{n}(\omega)xn=ξn(ω) для всех n ≥ 1 n ≥ 1 n >= 1n \geq 1n≥1, то из него (неравенства) следует, что
P ( | x n − x | ≤ ε ) > 1 − δ . P x n − x ≤ ε > 1 − δ . P(|x_(n)-x| <= epsi) > 1-delta.P\left(\left|x_{n}-x\right| \leq \varepsilon\right)>1-\delta .P(|xn−x|≤ε)>1−δ.
Это неравенство допускает важную частотную интерпретацию. Оно означает, что при n > n ( δ , ε ) n > n ( δ , ε ) n > n(delta,epsi)n>n(\delta, \varepsilon)n>n(δ,ε) относительная частота события | x − x n | ≤ ε x − x n ≤ ε |x-x_(n)| <= epsi\left|x-x_{n}\right| \leq \varepsilon|x−xn|≤ε будет не меньше, чем 1 − δ 1 − δ 1-delta1-\delta1−δ. Однако, это не означает, что равенство lim n → + ∞ x n = x lim n → + ∞   x n = x lim_(n rarr+oo)x_(n)=x\lim _{n \rightarrow+\infty} x_{n}=xlimn→+∞xn=x выполняется для всех ω ∈ Ω ω ∈ Ω omega in Omega\omega \in \Omegaω∈Ω.
(1.7.1) Пусть ( ξ z ) z ∈ Z 2 ξ z z ∈ Z 2 (xi_(z))_(z inZ^(2))\left(\xi_{z}\right)_{z \in Z^{2}}(ξz)z∈Z2 - однородное случайное поле со средним значением m m mmm и ковариационной функцией r , A n ⊂ Z 2 r , A n ⊂ Z 2 r,A_(n)subZ^(2)r, A_{n} \subset Z^{2}r,An⊂Z2 - квадрат со стороной n n nnn и x A n x A n x_(A_(n))x_{A_{n}}xAn - изображение. Для того, чтобы последовательность m n m n m_(n)m_{n}mn случайных величин, определяемая равенством
m n = 1 | A n | ∑ a ∈ A n ξ a m n = 1 A n ∑ a ∈ A n   ξ a m_(n)=(1)/(|A_(n)|)sum_(a inA_(n))xi_(a)m_{n}=\frac{1}{\left|A_{n}\right|} \sum_{a \in A_{n}} \xi_{a}mn=1|An|∑a∈Anξa
сходилась в среднем квадратичном к m m mmm при n → + ∞ n → + ∞ n rarr+oon \rightarrow+\inftyn→+∞, необходимо и достаточно, чтобы числовая последовательность
1 | A n | ∑ a ∈ A n r ( a ) 1 A n ∑ a ∈ A n   r ( a ) (1)/(|A_(n)|)sum_(a inA_(n))r(a)\frac{1}{\left|A_{n}\right|} \sum_{a \in A_{n}} r(a)1|An|∑a∈Anr(a)
сходилась к нулю при n → + ∞ n → + ∞ n rarr+oon \rightarrow+\inftyn→+∞.
Доказательство необходимости.
| 1 | A n | ∑ a ∈ A n r ( a ) | = | 1 | A n | ∑ a ∈ A n r ( a − 0 ) | = | 1 | A n | ∑ a ∈ A n E ( ξ a − m ) ( ξ 0 − m ) | ≤ ≤ | E ( ( ξ 0 − m ) | A n | ∑ a ∈ A n ( ξ a − m ) ) | = | E ( m n − m ) ( ξ 0 − m ) | ≤ 1 A n ∑ a ∈ A n   r ( a ) = 1 A n ∑ a ∈ A n   r ( a − 0 ) = 1 A n ∑ a ∈ A n   E ξ a − m ξ 0 − m ≤ ≤ E ξ 0 − m A n ∑ a ∈ A n   ξ a − m = E m n − m ξ 0 − m ≤ {:[|(1)/(|A_(n)|)sum_(a inA_(n))r(a)|=|(1)/(|A_(n)|)sum_(a inA_(n))r(a-0)|=|(1)/(|A_(n)|)sum_(a inA_(n))E(xi_(a)-m)(xi_(0)-m)| <= ],[ <= |E(((xi_(0)-m))/(|A_(n)|)sum_(a inA_(n))(xi_(a)-m))|=|E(m_(n)-m)(xi_(0)-m)| <= ]:}\begin{gathered} \left|\frac{1}{\left|A_{n}\right|} \sum_{a \in A_{n}} r(a)\right|=\left|\frac{1}{\left|A_{n}\right|} \sum_{a \in A_{n}} r(a-0)\right|=\left|\frac{1}{\left|A_{n}\right|} \sum_{a \in A_{n}} E\left(\xi_{a}-m\right)\left(\xi_{0}-m\right)\right| \leq \\ \leq\left|E\left(\frac{\left(\xi_{0}-m\right)}{\left|A_{n}\right|} \sum_{a \in A_{n}}\left(\xi_{a}-m\right)\right)\right|=\left|E\left(m_{n}-m\right)\left(\xi_{0}-m\right)\right| \leq \end{gathered}|1|An|∑a∈Anr(a)|=|1|An|∑a∈Anr(a−0)|=|1|An|∑a∈AnE(ξa−m)(ξ0−m)|≤≤|E((ξ0−m)|An|∑a∈An(ξa−m))|=|E(mn−m)(ξ0−m)|≤
≤ E ( m n − m ) 2 E ( ξ 0 − m ) 2 ≤ E m n − m 2 E ξ 0 − m 2 <= sqrt(E(m_(n)-m)^(2)E(xi_(0)-m)^(2))\leq \sqrt{E\left(m_{n}-m\right)^{2} E\left(\xi_{0}-m\right)^{2}}≤E(mn−m)2E(ξ0−m)2
По предположению m n → m m n → m m_(n)rarr mm_{n} \rightarrow mmn→m в ср. кв. при n → + ∞ n → + ∞ n rarr+oon \rightarrow+\inftyn→+∞. Поэтому для любого ε > 0 ε > 0 epsi > 0\varepsilon>0ε>0 существует n ( ε ) n ( ε ) n(epsi)n(\varepsilon)n(ε) такой, что для всех n > n ( ε ) n > n ( ε ) n > n(epsi)n>n(\varepsilon)n>n(ε) выполняется неравенство
E ( m n − m ) 2 < ε 2 E ( ξ 0 − m ) 2 E m n − m 2 < ε 2 E ξ 0 − m 2 E(m_(n)-m)^(2) < (epsi^(2))/(E(xi_(0)-m)^(2))E\left(m_{n}-m\right)^{2}<\frac{\varepsilon^{2}}{E\left(\xi_{0}-m\right)^{2}}E(mn−m)2<ε2E(ξ0−m)2
Из него следует, что при n > n ( ε ) n > n ( ε ) n > n(epsi)n>n(\varepsilon)n>n(ε) выполняется неравенство
1 | A n | ∑ a ∈ A n r ( a ) ≤ | 1 | A n | ∑ a ∈ A n r ( a ) | ≤ ε , 1 A n ∑ a ∈ A n   r ( a ) ≤ 1 A n ∑ a ∈ A n   r ( a ) ≤ ε , (1)/(|A_(n)|)sum_(a inA_(n))r(a) <= |(1)/(|A_(n)|)sum_(a inA_(n))r(a)| <= epsi,\frac{1}{\left|A_{n}\right|} \sum_{a \in A_{n}} r(a) \leq\left|\frac{1}{\left|A_{n}\right|} \sum_{a \in A_{n}} r(a)\right| \leq \varepsilon,1|An|∑a∈Anr(a)≤|1|An|∑a∈Anr(a)|≤ε,
Означающее, что
1 | A n | ∑ a ∈ A n r ( a ) 1 A n ∑ a ∈ A n   r ( a ) (1)/(|A_(n)|)sum_(a inA_(n))r(a)\frac{1}{\left|A_{n}\right|} \sum_{a \in A_{n}} r(a)1|An|∑a∈Anr(a)
сходится к нулю при n → + ∞ n → + ∞ n rarr+oon \rightarrow+\inftyn→+∞.
Достаточность. Из определения m n m n m_(n)m_{n}mn следует, что среднее значение E m n E m n Em_(n)E m_{n}Emn равняется m m mmm :
E m n = E ( 1 | A n | ∑ a ∈ A n ξ a ) = m E m n = E 1 A n ∑ a ∈ A n   ξ a = m Em_(n)=E((1)/(|A_(n)|)sum_(a inA_(n))xi_(a))=mE m_{n}=E\left(\frac{1}{\left|A_{n}\right|} \sum_{a \in A_{n}} \xi_{a}\right)=mEmn=E(1|An|∑a∈Anξa)=m
Оценки с такими свойствами называются несмещенными. Так как m n → m m n → m m_(n)rarr mm_{n} \rightarrow mmn→m в ср. кв., то
E ( 1 | A n | ∑ a ∈ A n ξ a − m ) 2 = 1 | A n | 2 E ( ∑ a ∈ A n ∑ b ∈ A n ( ξ a − m ) ( ξ b − m ) ) = = 1 | A n | 2 ∑ a ∈ A n ∑ b ∈ A n E ( ξ a − m ) ( ξ b − m ) = 1 | A n | 2 ∑ a ∈ A n ∑ b ∈ A n : a − b ∈ A n r ( a − b ) = E 1 A n ∑ a ∈ A n   ξ a − m 2 = 1 A n 2 E ∑ a ∈ A n   ∑ b ∈ A n   ξ a − m ξ b − m = = 1 A n 2 ∑ a ∈ A n   ∑ b ∈ A n   E ξ a − m ξ b − m = 1 A n 2 ∑ a ∈ A n   ∑ b ∈ A n : a − b ∈ A n   r ( a − b ) = {:[E((1)/(|A_(n)|)sum_(a inA_(n))xi_(a)-m)^(2)=(1)/(|A_(n)|^(2))E(sum_(a inA_(n))sum_(b inA_(n))(xi_(a)-m)(xi_(b)-m))=],[=(1)/(|A_(n)|^(2))sum_(a inA_(n))sum_(b inA_(n))E(xi_(a)-m)(xi_(b)-m)=(1)/(|A_(n)|^(2))sum_(a inA_(n))sum_(b inA_(n):a-b inA_(n))r(a-b)=]:}\begin{aligned} & E\left(\frac{1}{\left|A_{n}\right|} \sum_{a \in A_{n}} \xi_{a}-m\right)^{2}=\frac{1}{\left|A_{n}\right|^{2}} E\left(\sum_{a \in A_{n}} \sum_{b \in A_{n}}\left(\xi_{a}-m\right)\left(\xi_{b}-m\right)\right)= \\ = & \frac{1}{\left|A_{n}\right|^{2}} \sum_{a \in A_{n}} \sum_{b \in A_{n}} E\left(\xi_{a}-m\right)\left(\xi_{b}-m\right)=\frac{1}{\left|A_{n}\right|^{2}} \sum_{a \in A_{n}} \sum_{b \in A_{n}: a-b \in A_{n}} r(a-b)= \end{aligned}E(1|An|∑a∈Anξa−m)2=1|An|2E(∑a∈An∑b∈An(ξa−m)(ξb−m))==1|An|2∑a∈An∑b∈AnE(ξa−m)(ξb−m)=1|An|2∑a∈An∑b∈An:a−b∈Anr(a−b)=
Следствие. Если r ( a ) → 0 r ( a ) → 0 r(a)rarr0r(a) \rightarrow 0r(a)→0 при | a | = ( a 1 2 + a 2 2 ) 1 2 → + ∞ | a | = a 1 2 + a 2 2 1 2 → + ∞ |a|=(a_(1)^(2)+a_(2)^(2))^((1)/(2))rarr+oo|a|=\left(a_{1}^{2}+a_{2}^{2}\right)^{\frac{1}{2}} \rightarrow+\infty|a|=(a12+a22)12→+∞, то
m n = 1 | A n | ∑ a ∈ A n ξ a m n = 1 A n ∑ a ∈ A n   ξ a m_(n)=(1)/(|A_(n)|)sum_(a inA_(n))xi_(a)m_{n}=\frac{1}{\left|A_{n}\right|} \sum_{a \in A_{n}} \xi_{a}mn=1|An|∑a∈Anξa
сходится в среднем квадратичном к m m mmm при n → + ∞ n → + ∞ n rarr+oon \rightarrow+\inftyn→+∞.
Доказательство. Так как r ( a ) → 0 r ( a ) → 0 r(a)rarr0r(a) \rightarrow 0r(a)→0 при | a | → + ∞ | a | → + ∞ |a|rarr+oo|a| \rightarrow+\infty|a|→+∞, то, для любого ε > 0 ε > 0 epsi > 0\varepsilon>0ε>0 существует такое a ε a ε a_(epsi)a_{\varepsilon}aε, что | r ( a ) | < ε | r ( a ) | < ε |r(a)| < epsi|r(a)|<\varepsilon|r(a)|<ε при всех | a | > | a ε | | a | > a ε |a| > |a_(epsi)||a|>\left|a_{\varepsilon}\right||a|>|aε|. Пусть
A n ( ε ) = { a ∈ A n : | a | > | a ε | } и M = max ∈ A n ∖ A n ( ε ) | r ( a ) | A n ( ε ) = a ∈ A n : | a | > a ε  и  M = max ∈ A n ∖ A n ( ε )   | r ( a ) | A_(n)(epsi)={a inA_(n):|a| > |a_(epsi)|}" и "M=max_(inA_(n)\\A_(n)(epsi))|r(a)|A_{n}(\varepsilon)=\left\{a \in A_{n}:|a|>\left|a_{\varepsilon}\right|\right\} \text { и } M=\max _{\in A_{n} \backslash A_{n}(\varepsilon)}|r(a)|An(ε)={a∈An:|a|>|aε|} и M=max∈An∖An(ε)|r(a)|
Тогда
| 1 | A n | ∑ a ∈ A n r ( a ) | = | 1 | A n | ( ∑ a ∈ A n ( ε ) r ( a ) + ∑ a ∈ A n ∖ A n ( ε ) r ( a ) ) ≤ 1 | A n | ( | A n ( ε ) | ε + | A n ∖ A n ( ε ) | M ) ≤ ε + | A n ∖ A n ( ε ) | M | A n | 1 A n ∑ a ∈ A n   r ( a ) = 1 A n ∑ a ∈ A n ( ε )   r ( a ) + ∑ a ∈ A n ∖ A n ( ε )   r ( a ) ≤ 1 A n A n ( ε ) ε + A n ∖ A n ( ε ) M ≤ ε + A n ∖ A n ( ε ) M A n {:[|(1)/(|A_(n)|)sum_(a inA_(n))r(a)|=|(1)/(|A_(n)|)(sum_(a inA_(n)(epsi))r(a)+sum_(a inA_(n)\\A_(n)(epsi))r(a)) <= :}],[(1)/(|A_(n)|)(|A_(n)(epsi)|epsi+|A_(n)\\A_(n)(epsi)|M) <= epsi+(|A_(n)\\A_(n)(epsi)|M)/(|A_(n)|)]:}\begin{gathered} \left|\frac{1}{\left|A_{n}\right|} \sum_{a \in A_{n}} r(a)\right|=\left\lvert\, \frac{1}{\left|A_{n}\right|}\left(\sum_{a \in A_{n}(\varepsilon)} r(a)+\sum_{a \in A_{n} \backslash A_{n}(\varepsilon)} r(a)\right) \leq\right. \\ \frac{1}{\left|A_{n}\right|}\left(\left|A_{n}(\varepsilon)\right| \varepsilon+\left|A_{n} \backslash A_{n}(\varepsilon)\right| M\right) \leq \varepsilon+\frac{\left|A_{n} \backslash A_{n}(\varepsilon)\right| M}{\left|A_{n}\right|} \end{gathered}|1|An|∑a∈Anr(a)|=|1|An|(∑a∈An(ε)r(a)+∑a∈An∖An(ε)r(a))≤1|An|(|An(ε)|ε+|An∖An(ε)|M)≤ε+|An∖An(ε)|M|An|
Числитель второго слагаемого является константой, а знаменатель стремится κ + ∞ κ + ∞ kappa+oo\kappa+\inftyκ+∞ при n → + ∞ n → + ∞ n rarr+oon \rightarrow+\inftyn→+∞. Следовательно,
1 | A n | ∑ a ∈ A n r ( a ) → 0 1 A n ∑ a ∈ A n   r ( a ) → 0 (1)/(|A_(n)|)sum_(a inA_(n))r(a)rarr0\frac{1}{\left|A_{n}\right|} \sum_{a \in A_{n}} r(a) \rightarrow 01|An|∑a∈Anr(a)→0
а m n → m m n → m m_(n)rarr mm_{n} \rightarrow mmn→m в ср. кв.

1.9 Проверка статистических гипотез

Определение статистической гипотезы. Примеры гипотез. Назначение выборки. Статистические критерии. Статистика для проверки гипотеза о виде распределения. Уровень значимости и критическая область.
Статистической гипотезой называется предположение о наличии у случайной величины или у нескольких случайных величин определенного свойства. Довольно часто проверяются гипотезы о виде распределения случайной величины, равенстве распределений двух и более случайных величин, об их независимости, а также гипотезы о свойствах числовых характеристик случайных величин. Для принятия гипотезы или отказа от нее используется информация о случайных величинах, содержащаяся в их выборках. Если выдвинутая гипотеза согласуется с информацией, содержащейся в выборках, то она принимается. В противном случае она отклоняется. Правило, в соответствии с которым гипотеза принимается или отвергается называется статистическим критерием. Одним из наиболее популярных статистических критериев является критерий, предложенный К. Пирсоном и получивший название χ 2 χ 2 chi^(2)\chi^{2}χ2 (хи квадрат). Ниже рассматривается пример его применения для проверки гипотезы о виде распределения случайной величины ξ ξ xi\xiξ. На основании исследования ее выборки ( x j ) 1 ≤ j ≤ n x j 1 ≤ j ≤ n (x_(j))_(1 <= j <= n)\left(x_{j}\right)_{1 \leq j \leq n}(xj)1≤j≤n требуется подтвердить или отклонить предположение о том, что распределение случайной величины ξ ξ xi\xiξ является равномерным на интервале [ a , b ] [ a , b ] [a,b][\mathrm{a}, \mathrm{b}][a,b].
Проверка гипотезы начинается с разбиения интервала [ a , b ] [ a , b ] [a,b][a, b][a,b] точками ( a j ) 1 ≤ j ≤ N + 1 , a = a 1 < ⋯ < a N + 1 = b a j 1 ≤ j ≤ N + 1 , a = a 1 < ⋯ < a N + 1 = b (a_(j))_(1 <= j <= N+1),a=a_(1) < cdots < a_(N+1)=b\left(a_{j}\right)_{1 \leq j \leq N+1}, a=a_{1}<\cdots<a_{N+1}=b(aj)1≤j≤N+1,a=a1<⋯<aN+1=b, на N N NNN непересекающихся подинтервалов [ a j , a j + 1 [ , 1 ≤ j < N a j , a j + 1 , 1 ≤ j < N [a_(j),a_(j+1)[,1 <= j < N:}\left[a_{j}, a_{j+1}\left[, 1 \leq j<N\right.\right.[aj,aj+1[,1≤j<N, и [ a N , a N + 1 ] a N , a N + 1 [a_(N),a_(N+1)]\left[a_{N}, a_{N+1}\right][aN,aN+1]. Затем для каждого подинтервала с левой границей a j a j a_(j)a_{j}aj определяется число n j n j n_(j)n_{j}nj элементов выборки, оказавшихся в нем. Очевидно, что должно выполняться равенство n 1 + ⋯ + n N = n n 1 + ⋯ + n N = n n_(1)+cdots+n_(N)=nn_{1}+\cdots+n_{N}=nn1+⋯+nN=n. На следующем шаге для каждого подинтервала вычисляется вероятность p j , 1 ≤ j ≤ N p j , 1 ≤ j ≤ N p_(j),1 <= j <= Np_{j}, 1 \leq j \leq Npj,1≤j≤N, с которой случайная величина ξ ξ xi\xiξ принимает значение из [ a j , a j + 1 [ a j , a j + 1 [ [a_(j),a_(j+1)[:}\left[a_{j}, a_{j+1}[\right.[aj,aj+1[. В соответствии с выдвинутой гипотезой ее распределение является равномерным на интервале [ a , b ] [ a , b ] [a,b][a, b][a,b]. Поэтому
p j = P ( a j ≤ ξ < a j + 1 ) = a j + 1 − a j b − a , 1 ≤ j ≤ N . p j = P a j ≤ ξ < a j + 1 = a j + 1 − a j b − a , 1 ≤ j ≤ N . p_(j)=P(a_(j) <= xi < a_(j+1))=(a_(j+1)-a_(j))/(b-a),1 <= j <= N.p_{j}=P\left(a_{j} \leq \xi<a_{j+1}\right)=\frac{a_{j+1}-a_{j}}{b-a}, 1 \leq j \leq N .pj=P(aj≤ξ<aj+1)=aj+1−ajb−a,1≤j≤N.
Далее определяется функция от выборки вида
X N − 1 2 = ∑ 1 ≤ j ≤ N ( n j − n p j ) 2 n p j = ∑ 1 ≤ j ≤ N n j 2 n p j − n , X N − 1 2 = ∑ 1 ≤ j ≤ N   n j − n p j 2 n p j = ∑ 1 ≤ j ≤ N   n j 2 n p j − n , X_(N-1)^(2)=sum_(1 <= j <= N)((n_(j)-np_(j))^(2))/(np_(j))=sum_(1 <= j <= N)(n_(j)^(2))/(np_(j))-n,X_{N-1}^{2}=\sum_{1 \leq j \leq N} \frac{\left(n_{j}-n p_{j}\right)^{2}}{n p_{j}}=\sum_{1 \leq j \leq N} \frac{n_{j}^{2}}{n p_{j}}-n,XN−12=∑1≤j≤N(nj−npj)2npj=∑1≤j≤Nnj2npj−n,
которая называется статистикой критерия. Она является случайной величиной. Доказано, что при верной гипотезе ее распределение стремится к распределению χ N − 1 2 χ N − 1 2 chi_(N-1)^(2)\chi_{N-1}^{2}χN−12 с ( N − 1 ) ( N − 1 ) (N-1)(N-1)(N−1) степенью свободы при n → + ∞ n → + ∞ n rarr+oon \rightarrow+\inftyn→+∞. Пусть α − α − alpha-\alpha-α− неотрицательное число, называемое уровнем значимости. Решая уравнение P ( χ N − 1 2 ≥ t α ) = α P χ N − 1 2 ≥ t α = α P(chi_(N-1)^(2) >= t_(alpha))=alphaP\left(\chi_{N-1}^{2} \geq t_{\alpha}\right)= \alphaP(χN−12≥tα)=α, определяют неотрицательное число t α t α t_(alpha)t_{\alpha}tα. При значениях α α alpha\alphaα близких к нулю (обычно α = 0.001 , 0.01 α = 0.001 , 0.01 alpha=0.001,0.01\alpha=0.001,0.01α=0.001,0.01 или 0.05 ) событие χ N − 1 2 ≥ t α χ N − 1 2 ≥ t α chi_(N-1)^(2) >= t_(alpha)\chi_{N-1}^{2} \geq t_{\alpha}χN−12≥tα нас наблюдается редко. Поэтому интервал [ t α , + ∞ [ t α , + ∞ [ [t_(alpha),+oo[:}\left[t_{\alpha},+\infty[\right.[tα,+∞[ часто называют критической областью. В соответствии с критерием хи квадрат для принятия гипотезы или ее отклонения требуется, используя выборку ( x j ) 1 ≤ j ≤ n x j 1 ≤ j ≤ n (x_(j))_(1 <= j <= n)\left(x_{j}\right)_{1 \leq j \leq n}(xj)1≤j≤n, вычислить значение статистики X N − 1 2 X N − 1 2 X_(N-1)^(2)X_{N-1}^{2}XN−12 и сравнить его с t α t α t_(alpha)t_{\alpha}tα. При наступлении события X N − 1 2 < t α X N − 1 2 < t α X_(N-1)^(2) < t_(alpha)X_{N-1}^{2}<t_{\alpha}XN−12<tα, имеющую высокую вероятность ( 1 − α 1 − α 1-alpha1-\alpha1−α ), гипотеза принимается. В противном случае, если произошло событие X N − 1 2 ≥ t α X N − 1 2 ≥ t α X_(N-1)^(2) >= t_(alpha)X_{N-1}^{2} \geq t_{\alpha}XN−12≥tα с низкой вероятностью α α alpha\alphaα, гипотеза отклоняется.
Критерий хи квадрат следует применять в тех случаях, когда n ≥ 50 n ≥ 50 n >= 50n \geq 50n≥50, а n j ≥ 5 , 1 ≤ j ≤ N n j ≥ 5 , 1 ≤ j ≤ N n_(j) >= 5,1 <= j <= Nn_{j} \geq 5,1 \leq j \leq Nnj≥5,1≤j≤N. Для решения уравнения P ( χ N − 1 2 ≥ t α ) = α P χ N − 1 2 ≥ t α = α P(chi_(N-1)^(2) >= t_(alpha))=alphaP\left(\chi_{N-1}^{2} \geq t_{\alpha}\right)=\alphaP(χN−12≥tα)=α использую таблицы распределения хи квадрат. Если число степеней свободы ( N − 1 ) > 30 ( N − 1 ) > 30 (N-1) > 30(N-1)>30(N−1)>30, то вместо распределения хи квадрат используется нормальное. Его среднее значение и дисперсия оцениваются по выборке.
Изложенные выше сведения будут применяться в Главе 4 для выявления значимых локальных максимумов гистограммы амплитуд.

2.1 Определение локально однородной сцены

Определение объектов. Внутренние и граничные точки проекций. Изображения сцены и объекта. Свойства случайных величин, принадлежащих разным объектам. Определение простого объекта. Отличие сложного объекта от простого. Отличия их гистограмм.
Информация о сцене, как правило, носит не детерминированный, а статистический характер. Поэтому при создании модели сцены естественно воспользоваться теоретико-вероятностным подходом. Далее считается, что сцена является счетным множеством элементов, называемых пикселями. Каждый пиксель включает пару целых чисел z = ( z 1 , z 1 ) ∈ Z 2 z = z 1 , z 1 ∈ Z 2 z=(z_(1),z_(1))inZ^(2)z=\left(z_{1}, z_{1}\right) \in Z^{2}z=(z1,z1)∈Z2, которые называются его координатами, и дискретную случайную величину ξ z ξ z xi_(z)\xi_{z}ξz. Все случайные величины ( ξ z ) z ∈ Z 2 ξ z z ∈ Z 2 (xi_(z))_(z inZ^(2))\left(\xi_{z}\right)_{z \in Z^{2}}(ξz)z∈Z2 определены на одном и том же вероятностном пространстве ( Ω , A , P ) ( Ω , A , P ) (Omega,A,P)(\Omega, \mathcal{A}, P)(Ω,A,P) и принимают значения из конечного множества Y = { 0 , 1 , … , | Y | − 1 } Y = { 0 , 1 , … , | Y | − 1 } Y={0,1,dots,|Y|-1}Y=\{0,1, \ldots,|Y|- 1\}Y={0,1,…,|Y|−1}. Таким образом, сцена является случайным полем. Пусть ω ω omega\omegaω - некоторое элементарное событие из Ω Ω Omega\OmegaΩ, а x z = ξ z ( ω ) x z = ξ z ( ω ) x_(z)=xi_(z)(omega)x_{z}=\xi_{z}(\omega)xz=ξz(ω) - значение случайной величины в z ∈ Z 2 z ∈ Z 2 z inZ^(2)z \in Z^{2}z∈Z2. Изображением сцены будет называться семейство x = ( x z ) z ∈ Z 2 x = x z z ∈ Z 2 x=(x_(z))_(z inZ^(2))x=\left(x_{z}\right)_{z \in Z^{2}}x=(xz)z∈Z2. Одним из примеров получения изображения сцены является регистрация отраженного или собственного электромагнитного излучения сцены в оптическом диапазоне с помощью оптико-электронной системы.
Пусть d d ddd - евклидово расстояние на Z 2 Z 2 Z^(2)Z^{2}Z2. Точки z z zzz и t t ttt из Z 2 Z 2 Z^(2)Z^{2}Z2 назовем соседями, если расстояние между ними равно единице: d ( z , t ) = 1 d ( z , t ) = 1 d(z,t)=1d(z, t)=1d(z,t)=1. Таким образом, у каждой точки четыре соседа. Расстоянием между конечными подмножествами A A AAA и B B BBB из Z 2 Z 2 Z^(2)Z^{2}Z2 назовем число d ( A , B ) d ( A , B ) d(A,B)d(A, B)d(A,B), определяемое равенством
d ( A , B ) = min a ∈ A , b ∈ B d ( a , b ) . d ( A , B ) = min a ∈ A , b ∈ B   d ( a , b ) . d(A,B)=min_(a in A,b in B)d(a,b).d(A, B)=\min _{a \in A, b \in B} d(a, b) .d(A,B)=mina∈A,b∈Bd(a,b).
Точка a a aaa, принадлежащая подмножеству A A AAA из Z 2 Z 2 Z^(2)Z^{2}Z2, будет называться граничной точкой A A AAA, если у нее существует сосед z z zzz из Z 2 ∖ A Z 2 ∖ A Z^(2)\\AZ^{2} \backslash AZ2∖A (не принадлежащий
A). Подмножество граничных точек множества A A AAA называется его границей и обозначается Fr A Fr A Fr_(A)\operatorname{Fr}_{A}FrA или Fr ( A ) Fr ( A ) Fr(A)\operatorname{Fr}(A)Fr(A). Остальные точки подмножества A A AAA будут называться внутренними. Все соседи внутренних точек принадлежат A A AAA. На рисунке 2.1.1 изображены три подмножества A , B A , B A,BA, BA,B и C C CCC. Их элементами являются пересечения прямых перпендикулярных линий. Подмножество A A AAA содержит пять
Рисунок 2.1.1 - Внутренние и граничные точки множества
точек. Одна из них внутренняя, а четыре точки, обозначенные ромбами - граничные. Подмножество B B BBB состоит из 16 внутренних и 20 граничных точек. Все четыре точки подмножества C C CCC являются граничными. Очевидно, что само множество Z 2 Z 2 Z^(2)Z^{2}Z2 состоит только из внутренних точек.
Подмножество B B BBB из Z 2 Z 2 Z^(2)Z^{2}Z2 назовем связным, если для любой пары точек z z zzz и t t ttt из B B BBB существует конечное семейство ( a j ) 1 ≤ j ≤ n a j 1 ≤ j ≤ n (a_(j))_(1 <= j <= n)\left(a_{j}\right)_{1 \leq j \leq n}(aj)1≤j≤n точек из B B BBB таких, что z = a 1 z = a 1 z=a_(1)z=a_{1}z=a1, t = a n t = a n t=a_(n)t=a_{n}t=an и d ( a j , a j + 1 ) = 1 , 1 ≤ j < n d a j , a j + 1 = 1 , 1 ≤ j < n d(a_(j),a_(j+1))=1,1 <= j < nd\left(a_{j}, a_{j+1}\right)=1,1 \leq j<nd(aj,aj+1)=1,1≤j<n. Подмножества, приведенные на рисунке 2.1.1, являются связными. Однако подмножество, являющееся суммой ( A + B A + B A+BA+ BA+B ), таковым не является. Подмножество A A AAA будет называться односвязным, если его дополнение A C = Z 2 ∖ A A C = Z 2 ∖ A A^(C)=Z^(2)\\AA^{C}=Z^{2} \backslash AAC=Z2∖A является связным.
Пусть A A AAA - конечное односвязное подмножество Z 2 Z 2 Z^(2)Z^{2}Z2. Семейство из | A | | A | |A||A||A| случайных величин ξ A = ( ξ a ) a ∈ A ξ A = ξ a a ∈ A xi_(A)=(xi_(a))_(a in A)\xi_{A}=\left(\xi_{a}\right)_{a \in A}ξA=(ξa)a∈A будет называться простым объектом с проекцией A A AAA, если оно является фрагментом некоторого однородного случайного поля со средним значением m A m A m_(A)m_{A}mA и ковариационной функцией r A r A r_(A)r_{A}rA. Поэтому среднее значение амплитуды и ее дисперсия у всех пикселей простого объекта одни и те же. Изображением простого объекта будет называться семейство x A = ( x z ) z ∈ A , x z ∈ Y x A = x z z ∈ A , x z ∈ Y x_(A)=(x_(z))_(z in A),x_(z)in Yx_{A}=\left(x_{z}\right)_{z \in A}, x_{z} \in YxA=(xz)z∈A,xz∈Y. Примером изображения простого объекта можно считать изображение вертолета, представленное на рисунке 2.1.2. Характерным признаком простого объекта является его гистограмма с ярко выраженным единственным локальным максимумом, приведенная на рисунке 2.1.2.
Рисунок 2.1.2 - Простой объект
Рисунок 2.1.3 - Гистограмма простого объекта
Довольно часто при решении прикладных задач приходится иметь дело с объектами ξ B ξ B xi_(B)\xi_{B}ξB, односвязная проекция B B BBB которых является объединением из n n nnn непересекающихся связных подмножеств ( B j ) 1 ≤ j ≤ n B j 1 ≤ j ≤ n (B_(j))_(1 <= j <= n)\left(B_{j}\right)_{1 \leq j \leq n}(Bj)1≤j≤n. При этом каждое семейство ( ξ B j ) 1 ≤ j ≤ n ξ B j 1 ≤ j ≤ n (xi_(B_(j)))_(1 <= j <= n)\left(\xi_{B_{j}}\right)_{1 \leq j \leq n}(ξBj)1≤j≤n случайных величин является простым объектом со своим средним значением m B j m B j m_(B_(j))m_{B_{j}}mBj и своей ковариационной функцией r B j r B j r_(B_(j))r_{B_{j}}rBj. Такие объекты ξ B ξ B xi_(B)\xi_{B}ξB будут называться составными или сложными объектами и обозначаться ξ B = ( ξ B j , 1 ≤ j ≤ n ) ξ B = ξ B j , 1 ≤ j ≤ n xi_(B)=(xi_(B_(j)),1 <= j <= n)\xi_{B}= \left(\xi_{B_{j}}, 1 \leq j \leq n\right)ξB=(ξBj,1≤j≤n). Если простые объекты ξ B i ξ B i xi_(B_(i))\xi_{B_{i}}ξBi и ξ B j ξ B j xi_(B_(j))\xi_{B_{j}}ξBj, входящие в сложный объект ξ B ξ B xi_(B)\xi_{B}ξB, оказались соседями: d ( B i , B j ) = 1 d B i , B j = 1 d(B_(i),B_(j))=1d\left(B_{i}, B_{j}\right)=1d(Bi,Bj)=1, то соответствующие им однородные случайные поля должны отличаться хотя бы одним из указанных числовых параметров. Изображением x B x B x_(B)x_{B}xB сложного объекта является объединение изображений x B j x B j x_(B_(j))x_{B_{j}}xBj, составляющих его простых объектов: x B = ( x B j , 1 ≤ j ≤ n ) x B = x B j , 1 ≤ j ≤ n x_(B)=(x_(B_(j)),1 <= j <= n)x_{B}=\left(x_{B_{j}}, 1 \leq j \leq n\right)xB=(xBj,1≤j≤n). В качестве примера изображения сложного объекта можно привести изображение легкового автомобиля на рисунке 2.1.4. Характерным признаком сложного объекта является присутствие у гистограммы его изображения, представленной на рисунке 2.1.5, двух и более локальных максимумов.
Рисунок 2.1.4 - Сложный объект
Рисунок 2.1.5 - Гистограмма сложного объекта
В частном случае объект может состоять только из одного пикселя. Такие объекты называются одноточечными.
Объекты ξ A ξ A xi_(A)\xi_{A}ξA и ξ B ξ B xi_(B)\xi_{B}ξB будут называться соседями, если d ( A , B ) = 1 d ( A , B ) = 1 d(A,B)=1d(A, B)=1d(A,B)=1. Предполагается, что проекции разных объектов не пересекаются. Если ξ A ξ A xi_(A)\xi_{A}ξA и ξ B − ξ B − xi_(B)-\xi_{B}-ξB− разные объекты, то для любых a ∈ A a ∈ A a in Aa \in Aa∈A и b ∈ B b ∈ B b in Bb \in Bb∈B случайные величины ξ a ξ a xi_(a)\xi_{a}ξa и ξ b ξ b xi_(b)\xi_{b}ξb считаются независимыми. Объединение проекций всех объектов равняется Z 2 Z 2 Z^(2)Z^{2}Z2. В теореме существования (2.2.1) из 2.2 будет доказано, что для задания сцен с перечисленными выше свойствами достаточно определить распределения вероятностей P Y A = ( p Y A ( x A ) ) x A ∈ Y A P Y A = p Y A x A x A ∈ Y A P_(Y^(A))=(p_(Y^(A))(x_(A)))_(x_(A)inY^(A))P_{Y^{A}}=\left(p_{Y^{A}}\left(x_{A}\right)\right)_{x_{A} \in Y^{A}}PYA=(pYA(xA))xA∈YA только для ее объектов.
Сцена считается заданной, если известно разбиение Z 2 Z 2 Z^(2)Z^{2}Z2 на проекции образующих сцену простых объектов, а также если для каждого простого объекта с проекцией A A AAA известно его среднее значение m A m A m_(A)m_{A}mA и ковариационная функция r A r A r_(A)r_{A}rA. Далее такие сцены будут называться локально однородными.

2.2 Теорема существования

Существование локально однородных сцен, сформулированное в предыдущем п. 2.2.1, доказывается в приводимой ниже теореме.
(2.2.1) Пусть на Z 2 Z 2 Z^(2)Z^{2}Z2 задано разбиение, состоящее из конечных попарно не пересекающихся подмножеств, называемых проекциями простых объектов, и пусть каждой проекции B B BBB поставлено в соответствие распределение вероятностей P Y B = ( p Y B ( x B ) ) x B ∈ Y B P Y B = p Y B x B x B ∈ Y B P_(Y^(B))=(p_(Y^(B))(x_(B)))_(x_(B)inY^(B))P_{Y^{B}}=\left(p_{Y^{B}}\left(x_{B}\right)\right)_{x_{B} \in Y^{B}}PYB=(pYB(xB))xB∈YB на Y B Y B Y^(B)Y^{B}YB. Тогда существует вероятностное пространство ( Ω , A , P Ω , A , P Omega,A,P\Omega, \mathcal{A}, PΩ,A,P ) и локально однородная сцена ( ξ z ) z ∈ Z 2 ξ z z ∈ Z 2 (xi_(z))_(z inZ^(2))\left(\xi_{z}\right)_{z \in Z^{2}}(ξz)z∈Z2 на Z 2 Z 2 Z^(2)Z^{2}Z2 такая, что
P { ω ∈ Ω : ξ B ( ω ) = x B } = p Y B ( x B ) P ω ∈ Ω : ξ B ( ω ) = x B = p Y B x B P{omega in Omega:xi_(B)(omega)=x_(B)}=p_(Y^(B))(x_(B))P\left\{\omega \in \Omega: \xi_{B}(\omega)=x_{B}\right\}=p_{Y^{B}}\left(x_{B}\right)P{ω∈Ω:ξB(ω)=xB}=pYB(xB)
для любой проекции B B BBB и для любого x B ∈ Y B x B ∈ Y B x_(B)inY^(B)x_{B} \in Y^{B}xB∈YB. Кроме того, если A A AAA и B B BBB - проекции разных объектов сцены, то при любых a ∈ A a ∈ A a in Aa \in Aa∈A и b ∈ B b ∈ B b in Bb \in Bb∈B случайные величины ξ a ξ a xi_(a)\xi_{a}ξa и ξ b ξ b xi_(b)\xi_{b}ξb независимы:
p Y { a , b } ( x a , x b ) = p Y { a } ( x a ) p Y { b } ( x b ) . p Y { a , b } x a , x b = p Y { a } x a p Y { b } x b . p_(Y^({a,b}))(x_(a),x_(b))=p_(Y^({a}))(x_(a))p_(Y^({b}))(x_(b)).p_{Y^{\{a, b\}}}\left(x_{a}, x_{b}\right)=p_{Y^{\{a\}}}\left(x_{a}\right) p_{Y^{\{b\}}}\left(x_{b}\right) .pY{a,b}(xa,xb)=pY{a}(xa)pY{b}(xb).
Доказательство. В соответствии с теоремой Колмогорова [57], для задания случайного поля на Z 2 Z 2 Z^(2)Z^{2}Z2 необходимо и достаточно построить на Z 2 Z 2 Z^(2)Z^{2}Z2 семейство согласованных конечномерных распределений. В случае локально однородных сцен это можно сделать следующим образом.
Пусть A A AAA - конечное подмножество Z 2 , ( B j ) j ∈ J A Z 2 , B j j ∈ J A Z^(2),(B_(j))_(j inJ_(A))Z^{2},\left(B_{j}\right)_{j \in J_{A}}Z2,(Bj)j∈JA - проекции простых объектов, такие, что
A ⊂ ∑ j ∈ J A B j и A ∩ B j ≠ ∅ , j ∈ J A . A ⊂ ∑ j ∈ J A   B j  и  A ∩ B j ≠ ∅ , j ∈ J A . A subsum_(j inJ_(A))B_(j)" и "A nnB_(j)!=O/,j inJ_(A).A \subset \sum_{j \in J_{A}} B_{j} \text { и } A \cap B_{j} \neq \varnothing, j \in J_{A} .A⊂∑j∈JABj и A∩Bj≠∅,j∈JA.
Тогда
A = A ∩ ( ∑ j ∈ J A B j ) = ∑ j ∈ J A ( A ∩ B j ) . A = A ∩ ∑ j ∈ J A   B j = ∑ j ∈ J A   A ∩ B j . A=A nn(sum_(j inJ_(A))B_(j))=sum_(j inJ_(A))(A nnB_(j)).A=A \cap\left(\sum_{j \in J_{A}} B_{j}\right)=\sum_{j \in J_{A}}\left(A \cap B_{j}\right) .A=A∩(∑j∈JABj)=∑j∈JA(A∩Bj).
Очевидно, что ( A ∩ B j ) ⊂ B j A ∩ B j ⊂ B j (A nnB_(j))subB_(j)\left(A \cap B_{j}\right) \subset B_{j}(A∩Bj)⊂Bj. Поставим в соответствие каждому подмножеству ( A ∩ B j ) A ∩ B j (A nnB_(j))\left(A \cap B_{j}\right)(A∩Bj) семейство P Y P Y P_(Y)P_{Y}PY AnB j = ( p Y j = p Y _(j)=(p_(Y):}_{j}=\left(p_{Y}\right.j=(pY AnB j ( X A ∩ B j ) ) j X A ∩ B j {:_(j)(X_(A nnB_(j))))\left._{j}\left(X_{A \cap B_{j}}\right)\right)j(XA∩Bj)) с помощью равенства
p Y A ∩ B j ( x A ∩ B j ) = ∑ x B ∖ A ∩ B j p Y B ( x B ) p Y A ∩ B j x A ∩ B j = ∑ x B ∖ A ∩ B j   p Y B x B p_(Y^(A nnB_(j)))(x_(A nnB_(j)))=sum_(x_(B\\A nnB_(j)))p_(Y^(B))(x_(B))p_{Y^{A \cap B_{j}}}\left(x_{A \cap B_{j}}\right)=\sum_{x_{B \backslash A \cap B_{j}}} p_{Y^{B}}\left(x_{B}\right)pYA∩Bj(xA∩Bj)=∑xB∖A∩BjpYB(xB)
и покажем, что оно является распределением на Y A ∩ B j Y A ∩ B j Y^(A nnB_(j))Y^{A \cap B_{j}}YA∩Bj. В самом деле,
∑ x A ∩ B j ∈ Y p Y ∩ B j p Y ∩ B j ( x A ∩ B j ) = ∑ x A ∩ B j ∈ Y   p Y ∩ B j p Y ∩ B j x A ∩ B j = sum_(x_(A nnB_(j))in Y)p_(Y nnB_(j))p_(Y nnB_(j))(x_(A nnB_(j)))=\sum_{x_{A \cap B_{j}} \in Y} p_{Y \cap B_{j}} p_{Y \cap B_{j}}\left(x_{A \cap B_{j}}\right)=∑xA∩Bj∈YpY∩BjpY∩Bj(xA∩Bj)=
∑ x A ∩ B j ∈ Y A ∩ B j ( ∑ x B ∖ A ∩ B j p Y B ( x B ) ) = ∑ x B ∈ Y B p Y B ( x B ) = 1 . ∑ x A ∩ B j ∈ Y A ∩ B j   ∑ x B ∖ A ∩ B j   p Y B x B = ∑ x B ∈ Y B   p Y B x B = 1 . sum_(x_(A nnB_(j))inY^(A nnB_(j)))(sum_(x_(B\\A nnB_(j)))p_(Y^(B))(x_(B)))=sum_(x_(B)inY^(B))p_(Y^(B))(x_(B))=1.\sum_{x_{A \cap B_{j}} \in Y^{A \cap B_{j}}}\left(\sum_{x_{B \backslash A \cap B_{j}}} p_{Y^{B}}\left(x_{B}\right)\right)=\sum_{x_{B} \in Y^{B}} p_{Y^{B}}\left(x_{B}\right)=1 .∑xA∩Bj∈YA∩Bj(∑xB∖A∩BjpYB(xB))=∑xB∈YBpYB(xB)=1.
Определим семейство P Y A = ( p Y A ( x A ) ) x A ∈ Y A P Y A = p Y A x A x A ∈ Y A P_(Y^(A))=(p_(Y^(A))(x_(A)))_(x_(A)inY^(A))P_{Y^{A}}=\left(p_{Y^{A}}\left(x_{A}\right)\right)_{x_{A} \in Y^{A}}PYA=(pYA(xA))xA∈YA с помощью равенства
p Y A ( x A ) = ∏ j ∈ J A p Y A ∩ B j ( x A ∩ B j ) p Y A x A = ∏ j ∈ J A   p Y A ∩ B j x A ∩ B j p_(Y^(A))(x_(A))=prod_(j inJ_(A))p_(Y^(A nnB_(j)))(x_(A nnB_(j)))p_{Y^{A}}\left(x_{A}\right)=\prod_{j \in J_{A}} p_{Y^{A \cap B_{j}}}\left(x_{A \cap B_{j}}\right)pYA(xA)=∏j∈JApYA∩Bj(xA∩Bj)
и покажем, что оно является распределением на Y A Y A Y^(A)Y^{A}YA. В самом деле
∑ x A ∈ Y A p Y A ( x A ) = ∑ ( x A ∩ B j ∈ Y A ∩ B j , j ∈ J A ) ( ∏ j ∈ J A p Y A ∩ B j ( x A ∩ B j ) ) = ∏ j ∈ J A ( ∑ x A ∩ B j ∈ Y p Y A ∩ B j A ∩ B j ( x A ∩ B j ) ) = 1 . ∑ x A ∈ Y A   p Y A x A = ∑ x A ∩ B j ∈ Y A ∩ B j , j ∈ J A   ∏ j ∈ J A   p Y A ∩ B j x A ∩ B j = ∏ j ∈ J A   ∑ x A ∩ B j ∈ Y   p Y A ∩ B j A ∩ B j x A ∩ B j = 1 . {:[sum_(x_(A)inY^(A))p_(Y^(A))(x_(A))=sum_((x_(A nnB_(j))inY^(A nnB_(j)),j inJ_(A)))(prod_(j inJ_(A))p_(Y^(A nnB_(j)))(x_(A nnB_(j))))=],[prod_(j inJ_(A))(sum_(x_(A nnB_(j))in Y)p_(Y^(A nnB_(j)))^(A nnB_(j))(x_(A nnB_(j))))=1.]:}\begin{gathered} \sum_{x_{A} \in Y^{A}} p_{Y^{A}}\left(x_{A}\right)=\sum_{\left(x_{A \cap B_{j}} \in Y^{A \cap B_{j}}, j \in J_{A}\right)}\left(\prod_{j \in J_{A}} p_{Y^{A \cap B_{j}}}\left(x_{A \cap B_{j}}\right)\right)= \\ \prod_{j \in J_{A}}\left(\sum_{x_{A \cap B_{j}} \in Y} p_{Y^{A \cap B_{j}}}{ }^{A \cap B_{j}}\left(x_{A \cap B_{j}}\right)\right)=1 . \end{gathered}∑xA∈YApYA(xA)=∑(xA∩Bj∈YA∩Bj,j∈JA)(∏j∈JApYA∩Bj(xA∩Bj))=∏j∈JA(∑xA∩Bj∈YpYA∩BjA∩Bj(xA∩Bj))=1.
Для доказательства выполнения условий согласованности для семейства конечномерных распределений выберем множество C C CCC на Z 2 Z 2 Z^(2)Z^{2}Z2, не пересекающееся с A A AAA. Для C C CCC также существует, как и для A A AAA, конечное семейство ( B j ) j ∈ J C B j j ∈ J C (B_(j))_(j inJ_(C))\left(B_{j}\right)_{j \in J_{C}}(Bj)j∈JC такое, что
C = ∑ j ∈ J C ( C ∩ B j ) . C = ∑ j ∈ J C   C ∩ B j . C=sum_(j inJ_(C))(C nnB_(j)).C=\sum_{j \in J_{C}}\left(C \cap B_{j}\right) .C=∑j∈JC(C∩Bj).
Поэтому определим на Y C Y C Y^(C)Y^{C}YC распределение P Y C = ( p Y c ( x C ) ) x C ∈ Y C P Y C = p Y c x C x C ∈ Y C P_(Y^(C))=(p_(Y)c(x_(C)))_(x_(C)inY^(C))P_{Y^{C}}=\left(p_{Y} c\left(x_{C}\right)\right)_{x_{C} \in Y^{C}}PYC=(pYc(xC))xC∈YC указанным выше способом
p Y C ( x C ) = ∏ j ∈ J C p Y C ∩ B j ( x C ∩ B j ) . p Y C x C = ∏ j ∈ J C   p Y C ∩ B j x C ∩ B j . p_(Y)C(x_(C))=prod_(j inJ_(C))p_(Y)_(C nnB_(j))(x_(C nnB_(j))).p_{Y} C\left(x_{C}\right)=\prod_{j \in J_{C}} p_{Y}{ }_{C \cap B_{j}}\left(x_{C \cap B_{j}}\right) .pYC(xC)=∏j∈JCpYC∩Bj(xC∩Bj).
Покажем, что при C ∩ A = ∅ C ∩ A = ∅ C nn A=O/C \cap A=\emptysetC∩A=∅ для любых x A x A x_(A)x_{A}xA и x C x C x_(C)x_{C}xC имеет место равенство
∑ x C ∈ Y C p Y ( A + C ) ( x ( A + C ) ) = p Y A ( x A ) , ∑ x C ∈ Y C   p Y ( A + C ) x ( A + C ) = p Y A x A , sum_(x_(C)inY^(C))p_(Y^((A+C)))(x_((A+C)))=p_(Y^(A))(x_(A)),\sum_{x_{C} \in Y^{C}} p_{Y^{(A+C)}}\left(x_{(A+C)}\right)=p_{Y^{A}}\left(x_{A}\right),∑xC∈YCpY(A+C)(x(A+C))=pYA(xA),
означающее выполнение условий согласованности. Так как
A + C = ∑ j ∈ J A ( A ∩ B j ) + ∑ j ∈ J C ( C ∩ B j ) , A + C = ∑ j ∈ J A   A ∩ B j + ∑ j ∈ J C   C ∩ B j , A+C=sum_(j inJ_(A))(A nnB_(j))+sum_(j inJ_(C))(C nnB_(j)),A+C=\sum_{j \in J_{A}}\left(A \cap B_{j}\right)+\sum_{j \in J_{C}}\left(C \cap B_{j}\right),A+C=∑j∈JA(A∩Bj)+∑j∈JC(C∩Bj),
TO
p Y ( A + C ) ( x ( A + C ) ) = ∏ j ∈ J A p Y A ∩ B j ( x A ∩ B j ) ∏ j ∈ J C p Y C ∩ B j ( x C ∩ B j ) . p Y ( A + C ) x ( A + C ) = ∏ j ∈ J A   p Y A ∩ B j x A ∩ B j ∏ j ∈ J C   p Y C ∩ B j x C ∩ B j . p_(Y)^((A+C))(x_((A+C)))=prod_(j inJ_(A))p_(Y^(A nnB_(j)))(x_(A nnB_(j)))prod_(j inJ_(C))p_(Y)_(C nnB_(j))(x_(C nnB_(j))).p_{Y}^{(A+C)}\left(x_{(A+C)}\right)=\prod_{j \in J_{A}} p_{Y^{A \cap B_{j}}}\left(x_{A \cap B_{j}}\right) \prod_{j \in J_{C}} p_{Y}{ }_{C \cap B_{j}}\left(x_{C \cap B_{j}}\right) .pY(A+C)(x(A+C))=∏j∈JApYA∩Bj(xA∩Bj)∏j∈JCpYC∩Bj(xC∩Bj).
Далее
∑ x C ∈ Y C p Y ( A + C ) ( x ( A + C ) ) = ∑ ( x C ∩ B j ∈ Y C C ∩ B j , j ∈ J C ) ∏ j ∈ J A p Y A ∩ B j ( x A ∩ B j ) ∏ j ∈ J C p Y C ∩ B j ( x C ∩ B j ) = ∏ j ∈ J A p Y A ∩ B j ( x A ∩ B j ) ∑ ( x C ∩ B j ∈ Y C ∩ B j , j ∈ J C ) ( ∏ j ∈ J C p Y C ∩ B j ( x C ∩ B j ) ) = ∏ j ∈ J A p Y A ∩ B j ( x A ∩ B j ) ∑ x C ∈ Y p Y C ( x C ) = p Y ( x A ) . ∑ x C ∈ Y C   p Y ( A + C ) x ( A + C ) = ∑ x C ∩ B j ∈ Y C C ∩ B j , j ∈ J C   ∏ j ∈ J A   p Y A ∩ B j x A ∩ B j ∏ j ∈ J C   p Y C ∩ B j x C ∩ B j = ∏ j ∈ J A   p Y A ∩ B j x A ∩ B j ∑ x C ∩ B j ∈ Y C ∩ B j , j ∈ J C   ∏ j ∈ J C   p Y C ∩ B j x C ∩ B j = ∏ j ∈ J A   p Y A ∩ B j x A ∩ B j ∑ x C ∈ Y   p Y C x C = p Y x A . {:[sum_(x_(C)in YC)p_(Y)(A+C)(x_((A+C)))=],[sum_((x_(C nnB_(j))in YC^(C nnB_(j)),j inJ_(C)))prod_(j inJ_(A))p_(Y)^(A nnB_(j))(x_(A nnB_(j)))prod_(j inJ_(C))p_(Y)^(C nnB_(j))(x_(C nnB_(j)))=],[prod_(j inJ_(A))p_(Y^(A nnB_(j)))(x_(A nnB_(j)))sum_((x_(C nnB_(j))inY^(C nnB_(j)),j inJ_(C)))(prod_(j inJ_(C))p_(Y)^(C nnB_(j))(x_(C nnB_(j))))=],[prod_(j inJ_(A))p_(Y^(A nnB_(j)))(x_(A nnB_(j)))sum_(x_(C)in Y)p_(Y)C(x_(C))=p_(Y)(x_(A)).]:}\begin{gathered} \sum_{x_{C} \in Y C} p_{Y}(A+C)\left(x_{(A+C)}\right)= \\ \sum_{\left(x_{C \cap B_{j}} \in Y C^{C \cap B_{j}}, j \in J_{C}\right)} \prod_{j \in J_{A}} p_{Y}^{A \cap B_{j}}\left(x_{A \cap B_{j}}\right) \prod_{j \in J_{C}} p_{Y}^{C \cap B_{j}}\left(x_{C \cap B_{j}}\right)= \\ \prod_{j \in J_{A}} p_{Y^{A \cap B_{j}}}\left(x_{A \cap B_{j}}\right) \sum_{\left(x_{C \cap B_{j}} \in Y^{C \cap B_{j}}, j \in J_{C}\right)}\left(\prod_{j \in J_{C}} p_{Y}^{C \cap B_{j}}\left(x_{C \cap B_{j}}\right)\right)= \\ \prod_{j \in J_{A}} p_{Y^{A \cap B_{j}}}\left(x_{A \cap B_{j}}\right) \sum_{x_{C} \in Y} p_{Y} C\left(x_{C}\right)=p_{Y}\left(x_{A}\right) . \end{gathered}∑xC∈YCpY(A+C)(x(A+C))=∑(xC∩Bj∈YCC∩Bj,j∈JC)∏j∈JApYA∩Bj(xA∩Bj)∏j∈JCpYC∩Bj(xC∩Bj)=∏j∈JApYA∩Bj(xA∩Bj)∑(xC∩Bj∈YC∩Bj,j∈JC)(∏j∈JCpYC∩Bj(xC∩Bj))=∏j∈JApYA∩Bj(xA∩Bj)∑xC∈YpYC(xC)=pY(xA).
Таким образом, если для каждого объекта ξ B ξ B xi_(B)\xi_{B}ξB задано распределение вероятностей P Y B = ( p Y B ( x B ) ) x B ∈ Y B P Y B = p Y B x B x B ∈ Y B P_(Y^(B))=(p_(Y^(B))(x_(B)))_(x_(B)inY^(B))P_{Y^{B}}=\left(p_{Y^{B}}\left(x_{B}\right)\right)_{x_{B} \in Y^{B}}PYB=(pYB(xB))xB∈YB, то существует случайное поле ( ξ z ) z ∈ Z 2 ξ z z ∈ Z 2 (xi_(z))_(z inZ^(2))\left(\xi_{z}\right)_{z \in Z^{2}}(ξz)z∈Z2 такое, что
P { ω : ( ξ b ( ω ) , b ∈ B ) = x B } = p Y B ( x B ) . P ω : ξ b ( ω ) , b ∈ B = x B = p Y B x B . P{omega:(xi_(b)(omega),b in B)=x_(B)}=p_(Y^(B))(x_(B)).P\left\{\omega:\left(\xi_{b}(\omega), b \in B\right)=x_{B}\right\}=p_{Y^{B}}\left(x_{B}\right) .P{ω:(ξb(ω),b∈B)=xB}=pYB(xB).
Независимость случайных величин ξ a ξ a xi_(a)\xi_{a}ξa и ξ b ξ b xi_(b)\xi_{b}ξb, принадлежащих разным проекциям A A AAA и B B BBB, следует непосредственно из определения конечномерных распределений. Пусть D = { a , b } D = { a , b } D={a,b}D=\{a, b\}D={a,b}. Так как A A AAA и B B BBB проекции, то их пересечение является пустым множеством. Кроме того, D ∩ A = { a } , D ∩ B = { b } D ∩ A = { a } , D ∩ B = { b } D nn A={a},D nn B={b}D \cap A=\{a\}, D \cap B=\{b\}D∩A={a},D∩B={b} и D ⊂ ( A + B ) D ⊂ ( A + B ) D sub(A+B)D \subset (A+B)D⊂(A+B). Поэтому
p Y D ( x D ) = p Y D ∩ A ( x D ∩ A ) p Y D ∩ B ( x D ∩ B ) = p Y { a } ( x a ) p Y { b } ( x b ) . p Y D x D = p Y D ∩ A x D ∩ A p Y D ∩ B x D ∩ B = p Y { a } x a p Y { b } x b . p_(Y^(D))(x_(D))=p_(Y^(D nn A))(x_(D nn A))p_(Y^(D nn B))(x_(D nn B))=p_(Y^({a}))(x_(a))p_(Y^({b}))(x_(b)).p_{Y^{D}}\left(x_{D}\right)=p_{Y^{D \cap A}}\left(x_{D \cap A}\right) p_{Y^{D \cap B}}\left(x_{D \cap B}\right)=p_{Y^{\{a\}}}\left(x_{a}\right) p_{Y^{\{b\}}}\left(x_{b}\right) .pYD(xD)=pYD∩A(xD∩A)pYD∩B(xD∩B)=pY{a}(xa)pY{b}(xb).
Таким образом, теорема существования доказана. Из нее следует, что построение скалярной сцены, с формальной точки зрения, сводится к разбиению Z 2 Z 2 Z^(2)Z^{2}Z2 на конечные подмножества (проекции образующих ее простых объектов) и заданию для каждой проекции A A AAA совместного распределения P Y A P Y A P_(Y)^(A)P_{Y}{ }^{A}PYA на Y A Y A Y^(A)Y^{A}YA.

2.3 Примеры сцен и изображений

В настоящей работе будут использоваться три вида сцен и изображений. Сценами первого типа служат различные участки поверхности Земли. Их изображения формируются оптико-электронными системами (в том числе многоспектральными). Поэтому такие сцены и их изображения называются далее реальными. Очевидно, что предположения, использованные при построении любой математической модели, для реальных сцен в полном объеме не выполняются. Однако хорошая модель должна быть "снисходительной" к некоторым нарушениям предположений, которые использовались при ее построении. В противном случае применимость модели для решения прикладных задач, в частности прогнозирования, становится сомнительной. Реальные используются для оценки адекватности математических моделей.
В качестве примера фрагмента реальной сцены предлагается квадратный участок земной поверхности. Он порос травой, редким кустарником и отдельными деревьями. На нем присутствуют следы, оставленные колесными и гусеничными транспортными средствами. В центре участка присутствует массивный стальной объект длиной 6 и шириной 3 м. На рисунках 2.3.1-2.3.3 представлены три скалярных изображения описанного фрагмента размером 256 на 256 пикселей. Они получены оптико-электронной системой строчного типа с механическим сканированием, расположенной на летательном аппарате. Съемка проводилась в диапазоне [ 0.7 ; 1.1 ] [ 0.7 ; 1.1 ] [0.7;1.1][0.7 ; 1.1][0.7;1.1] мкм (рисунок 2.3.1), [3.0;5.0] мкм (рисунок 2.3.2) и [8.0;12.0] мкм (рисунок 2.3.3). По условиям съемки, длина стороны квадратного пикселя на местности должна равняться 0.3 м. На изображениях (в основном на третьем) заметны горизонтальные полосы. Эта особенность, называемая специалистами строчностью, характерна для изображений, формируемых первыми оптико-электронными системами строчного типа с механическим сканированием.
К сожалению, в ходе съемки с целью получения векторного (трехмер-
ного) изображения сцены не удалось обеспечить выполнение ряда важных требований. Например, для регистрации скалярных изображений, формируемых в трех спектральных зонах, над сценой приходилось пролетать два или три раза. Промежуток времени между следующими друг за другом пролетами равнялся нескольким минутам. Предполагалось, что за это время метеоусловия и состояние объектов, не успеют измениться. Из-за погрешностей бортовых высотомеров линейные размеры пикселей на местности получились разными. Поэтому размеры изображений одних и тех же объектов сцены на разных скалярных компонентах оказались различными. Более того, выполнить все полеты по одной и той же траектории не удалось. По этой причине скалярные изображения отличаются друг от друга величиной сдвига и поворота. Таким образом, для получения векторного (в данном случае трехмерного) изображения фрагмента сцены и его последующего использования в экспериментах по дешифрированию требуется предварительно привести скалярные компоненты к одному масштабу и выполнить их пространственное совмещение, включающее поворот и сдвиг. Необходимо отметить, что современное оборудование
Рисунок 2.3.1 - Первая компонента. Диапазон [ 0.7 ; 1.1 ] [ 0.7 ; 1.1 ] [0.7;1.1][0.7 ; 1.1][0.7;1.1] мкм
Рисунок 2.3.2 - Вторая компонента. Диапазон [ 3.0 ; 5.0 ] [ 3.0 ; 5.0 ] [3.0;5.0][3.0 ; 5.0][3.0;5.0] мкм
Рисунок 2.3.3 - Третья компонента. Диапазон [ 8.0 ; 12.0 ] [ 8.0 ; 12.0 ] [8.0;12.0][8.0 ; 12.0][8.0;12.0] мкм
позволяет получать многоспектральные изображения, насчитывающие сотни компонент. Такие изображения получили название гиперспектральных.
Довольно часто в компьютерных экспериментах используются изображения реальных сцен после внесения в них тех или иных изменений. Такая модификация применяется, в частности, для добавления на изображение объектов, отсутствующих на исходном изображении. За свое сходство с реальными изображениями модифицированные изображения будут называться квазиреальными. В качестве примера на рисунках 2.3.4-2.3.6 приведены три квазиреальных изображения. Они получены в результате добавления изображений восьми дополнительных объектов, отсутствовавших сцене, с помощью компьютера на изображения, приведенные на рисунках 2.3.1-2.3.3. Изображения добавленных объектов имеют прямоугольную форму, случайные координаты и ориентацию. Их размеры совпадают с размерами реальных объектов. Предполагается, что каждый объект является фрагментом однородного случайного поля. В качестве средних значений и дисперсий добавленных объектов служат оценки соответствующих параметров, подсчитанные по реальным изображениям. Рядом с изображением каждого добавленного объекта указан его порядковый номер.
К третьему типу относятся локально однородные сцены с заранее заданными свойствами, которые используются для тестирования правильности работы алгоритмов. Их изображения строятся компьютерами. В качестве примера на рисунках 2.3.7, 2.3.8 и 2.3.9 приведены квадратные фрагменты со стороной 256 пикселей изображений однородных случайных полей. Они получены скользящим суммированием с r ^ = 0 , r ^ = 1 r ^ = 0 , r ^ = 1 hat(r)=0, hat(r)=1\hat{r}=0, \hat{r}=1r^=0,r^=1 и r ^ = 2 r ^ = 2 hat(r)=2\hat{r}=2r^=2 соответственно. Каждый фрагмент состоит из семи объектов. Шесть объектов имеют прямоугольные проекции со сторонами 29 и 14 пикселей, случайную ориентацию и месторасположение. Пять из них присутствуют на приводимом фрагменте полностью. Шестой объект, находящийся у левого края фрагмента, присутствует частично. Остальные пиксели фрагмента образуют седьмой объект, ко-
торый по сложившейся среди специалистов по дешифрированию изображений традиции будет называться фоном. Признаком пикселя во всех экспериментах служила амплитуда со значениями из множества Y = { 0 , … , 255 } Y = { 0 , … , 255 } Y={0,dots,255}Y=\{0, \ldots, 255\}Y={0,…,255}.
Рисунок 2.3.4 - Первая квазиреальная компонента
Рисунок 2.3.5 - Вторая квазиреальная компонента
Рисунок 2.3.6 - Третья квазиреальная компонента
Рисунок 2.3.7 - Изображение локально однородной сцены с взаимно независимыми случайными величинами
Рисунок 2.3.8 - Изображение локально однородной сцены, полученной скользящим суммированием с r ^ = 1 r ^ = 1 hat(r)=1\hat{r}=1r^=1
Рисунок 2.3.9 - Изображение локально однородной сцены, полученной скользящим суммированием с r ^ = 2 r ^ = 2 hat(r)=2\hat{r}=2r^=2

2.4 Сглаживание и шум

Определение и характеристики аддитивного шума. Измерение шума по изображению.
Каждый элемент матрицы ФПУ преобразует воздействующее на него электромагнитное излучение в цифровой электрический сигнал. Этот сигнал подвергается обязательному усилению, возможно, еще каким-либо заранее запланированным воздействиям и, наконец, устройством отображения (например, дисплеем) преобразуется в электромагнитное изучение видимого диапазона для визуального анализа или записывается на тот или иной носитель информации. К сожалению, в ходе своего «путешествия» по ОЭС кроме запланированных преобразований электрический сигнал испытывает также неконтролируемым воздействиям различных ее элементов. Совокупность таких воздействий, вызывающих изменения электрического сигнала, принято называть шумом.
Наиболее простым видом шума является аддитивны гауссовский шум. С формальной точки зрения такой шум является случайным полем. Образующие его случайные величины независимы в совокупности и имеют одно и то же нормальное распределение с нулевым средним и отличным от нуля среднеквадратическим отклонением. При использовании аддитивного гауссовского шума сцена ξ = ( ξ z ) ξ = ξ z xi=(xi_(z))\xi=\left(\xi_{z}\right)ξ=(ξz) рассматривается в виде суммы двух неизвестных слагаемых. Одним слагаемым является детерминированная функция y = ( y z ) y = y z y=(y_(z))y=\left(y_{z}\right)y=(yz), описывающая свойства каждого пикселя сцены. Вторым слагаемым служит шум η = ( η z ) η = η z eta=(eta_(z))\eta=\left(\eta_{z}\right)η=(ηz), который является случайным полем.
На рисунке 2.4.1 приведен фрагмент изображения, полученного камерой сотового телефона в темной комнате (при отсутствии какого-либо освещения), а на рисунке 2.4.2 - этот же фрагмент, но после линейного контрастирования.
Пуст r r rrr - натуральное число, сглаживанием с радиусом r r rrr изображения x D = ( x z ) z ∈ D x D = x z z ∈ D x_(D)=(x_(z))_(z in D)x_{D}=\left(x_{z}\right)_{z \in D}xD=(xz)z∈D будет называться операция получения изображения x ^ D = ( x ^ z ) z ∈ D x ^ D = x ^ z z ∈ D hat(x)_(D)=( hat(x)_(z))_(z in D)\hat{x}_{D}= \left(\hat{x}_{z}\right)_{z \in D}x^D=(x^z)z∈D, определяемая следующим образом
x ^ z = 1 | B ( z , r ) ∩ D | ∑ t ∈ B ( z , r ) ∩ D x t , z ∈ D . x ^ z = 1 | B ( z , r ) ∩ D | ∑ t ∈ B ( z , r ) ∩ D   x t , z ∈ D . hat(x)_(z)=(1)/(|B(z,r)nn D|)sum_(t in B(z,r)nn D)x_(t),z in D.\hat{x}_{z}=\frac{1}{|B(z, r) \cap D|} \sum_{t \in B(z, r) \cap D} x_{t}, z \in D .x^z=1|B(z,r)∩D|∑t∈B(z,r)∩Dxt,z∈D.
Изображение x ^ D x ^ D hat(x)_(D)\hat{x}_{D}x^D, полученное в результате сглаживания, называется сглаженным.

Глава 3 ПРИЗНАКИ ОБЪЕКТОВ

Образующие сцену объекты могут отличаться довольно высоким разнообразием. При этом считается нормой, когда в изображениях разных объектов присутствуют пиксели с одинаковыми амплитудами. Это означает, что решение задачи обнаружения и классификации объектов только за счет использования амплитуд (иногда их называют прямыми признаками) является скорее исключением, а не нормой. Отдавая должное роли признаков, им уделяется отдельная глава.
В 3.1 обсуждается формальное определение признака объекта как отображения, заданного на множестве всех его изображений и удовлетворяющего некоторым естественным требованиям. Показывается, что класс таких отображений (признаков) достаточно широк.
При визуальном дешифрировании изображений форма присутствующих на сцене объектов является важным демаскирующим признаком, применяемым зачастую на подсознательном уровне. Для применение этого признака при автоматическом дешифрировании требуется его формальное определение. Несмотря на довольно большое число публикаций, посвященных изложению различных способов формализации понятия формы (см., например [49, 50, 6971]), исследования в этом направлении, по-прежнему, сохраняют свою актуальность. Этому признаку посвящается п. 3.2.
В п. 3.3 формулируется байесовская постановка задачи классификации объектов и вид оптимального решающего правила.

3.1 Формализация признаков

Определение признака. Примеры признаков: амплитуда пикселя, среднее арифметическое амплитуд проекции, площадь объекта.
Для каждого элементарного события ω ∈ Ω ω ∈ Ω omega in Omega\omega \in \Omegaω∈Ω объект ξ A = ( ξ a ) ∈ A ξ A = ξ a ∈ A xi_(A)=(xi_(a))_(in A)\xi_{A}=\left(\xi_{a}\right)_{\in A}ξA=(ξa)∈A определяет с помощью равенства x a = ξ a ( ω ) , a ∈ A x a = ξ a ( ω ) , a ∈ A x_(a)=xi_(a)(omega),a in Ax_{a}=\xi_{a}(\omega), a \in Axa=ξa(ω),a∈A, изображение x A = ( x a ) a ∈ A x A = x a a ∈ A x_(A)=(x_(a))_(a in A)x_{A}=\left(x_{a}\right)_{a \in A}xA=(xa)a∈A. Оно является элементом множества Y A = { ( x a ) a ∈ A : x a ∈ Y } Y A = x a a ∈ A : x a ∈ Y Y^(A)={(x_(a))_(a in A):x_(a)in Y}Y^{A}=\left\{\left(x_{a}\right)_{a \in A}: x_{a} \in Y\right\}YA={(xa)a∈A:xa∈Y} всех возможных изображений объекта ξ A ξ A xi_(A)\xi_{A}ξA. Следовательно, ξ A ξ A xi_(A)\xi_{A}ξA является отображением типа Ω → Y A Ω → Y A Omega rarrY^(A)\Omega \rightarrow Y^{A}Ω→YA.
Для сравнения свойств различных объектов определим на множестве Y A Y A Y^(A)Y^{A}YA изображений каждого объекта ξ A ξ A xi_(A)\xi_{A}ξA отображение f A : Y A → R f A : Y A → R f_(A):Y^(A)rarr Rf_{A}: Y^{A} \rightarrow RfA:YA→R. Очевидно, что суперпозиция f A ∘ ξ A f A ∘ ξ A f_(A)@xi_(A)f_{A} \circ \xi_{A}fA∘ξA, определяемая равенством ( f A ∘ ξ A ) ( ω ) = f A ( ξ A ( ω ) ) f A ∘ ξ A ( ω ) = f A ξ A ( ω ) (f_(A)@xi_(A))(omega)=f_(A)(xi_(A)(omega))\left(f_{A} \circ \xi_{A}\right)(\omega)=f_{A}\left(\xi_{A}(\omega)\right)(fA∘ξA)(ω)=fA(ξA(ω)), является отображением типа Ω → R Ω → R Omega rarr R\Omega \rightarrow RΩ→R. При теоретико-вероятностном подходе к задаче дешифрирования естественно потребовать, чтобы суперпозиция f A ∘ ξ A f A ∘ ξ A f_(A)@xi_(A)f_{A} \circ \xi_{A}fA∘ξA была случайной величиной. Известно, что случайные величины образуют довольно широкий класс отображений. Вместе с тем, также известно, что не каждое отображение вида Ω → R Ω → R Omega rarr R\Omega \rightarrow RΩ→R является случайной величиной. Что касается рассматриваемого случая, то ответ содержится в следующей теореме [67, с. 59].
(3.1.1) Если f A : R n → R f A : R n → R f_(A):R^(n)rarr Rf_{A}: R^{n} \rightarrow RfA:Rn→R является борелевским отображением, то суперпозиция f A ∘ ξ A f A ∘ ξ A f_(A)@xi_(A)f_{A} \circ \xi_{A}fA∘ξA является случайной величиной на вероятностном пространстве ( Ω , A , P Ω , A , P Omega,A,P\Omega, \mathcal{A}, PΩ,A,P ).
Доказательство. Пусть B B BBB - борелевское подмножество из R R RRR. Тогда его прообраз ( f A ∘ ξ A ) − 1 ( B ) f A ∘ ξ A − 1 ( B ) (f_(A)@xi_(A))^(-1)(B)\left(f_{A} \circ \xi_{A}\right)^{-1}(B)(fA∘ξA)−1(B) принимает вид
( f A ∘ ξ A ) − 1 ( B ) = { ω : f A ( ξ A ( ω ) ) ∈ B } = { ω : ξ A ( ω ) ∈ f A − 1 ( B ) } = { ω : ξ A − 1 ( f A − 1 ( B ) ) } f A ∘ ξ A − 1 ( B ) = ω : f A ξ A ( ω ) ∈ B = ω : ξ A ( ω ) ∈ f A − 1 ( B ) = ω : ξ A − 1 f A − 1 ( B ) {:[(f_(A)@xi_(A))^(-1)(B)={omega:f_(A)(xi_(A)(omega))in B}=],[{omega:xi_(A)(omega)inf_(A)^(-1)(B)}={omega:xi_(A)^(-1)(f_(A)^(-1)(B))}]:}\begin{gathered} \left(f_{A} \circ \xi_{A}\right)^{-1}(B)=\left\{\omega: f_{A}\left(\xi_{A}(\omega)\right) \in B\right\}= \\ \left\{\omega: \xi_{A}(\omega) \in f_{A}^{-1}(B)\right\}=\left\{\omega: \xi_{A}^{-1}\left(f_{A}^{-1}(B)\right)\right\} \end{gathered}(fA∘ξA)−1(B)={ω:fA(ξA(ω))∈B}={ω:ξA(ω)∈fA−1(B)}={ω:ξA−1(fA−1(B))}
По условиям теоремы f A − 1 ( B ) f A − 1 ( B ) f_(A)^(-1)(B)f_{A}^{-1}(B)fA−1(B) - борелевское подмножество в R | A | , ξ A − R | A | , ξ A − R^(|A|),xi_(A)-R^{|A|}, \xi_{A}-R|A|,ξA− векторная ( | A | | A | |A||A||A| - мерная) случайная величина|. Поэтому ξ A − 1 ( f A − 1 ( B ) ) ξ A − 1 f A − 1 ( B ) xi_(A)^(-1)(f_(A)^(-1)(B))\xi_{A}^{-1}\left(f_{A}^{-1}(B)\right)ξA−1(fA−1(B)) из Ω Ω Omega\OmegaΩ является подмножеством A A A\mathcal{A}A, а f A ∘ ξ A f A ∘ ξ A f_(A)@xi_(A)f_{A} \circ \xi_{A}fA∘ξA - случайной величиной на ( Ω , A , P Ω , A , P Omega,A,P\Omega, \mathcal{A}, PΩ,A,P ).
Далее борелевское отображение f A : R n → R f A : R n → R f_(A):R^(n)rarr Rf_{A}: R^{n} \rightarrow RfA:Rn→R, определенное на множестве Y A Y A Y^(A)Y^{A}YA изображений объекта ξ A ξ A xi_(A)\xi_{A}ξA, будет называться его признаком, а распределение случайной величины f A ∘ ξ A − f A ∘ ξ A − f_(A)@xi_(A)-f_{A} \circ \xi_{A}-fA∘ξA− распределением признака f A f A f_(A)f_{A}fA с соответствующими средним значением, дисперсией и другими числовыми характеристиками. Известно (например, [XX]), что каждая непрерывная функция является борелевской. Поэтому класс возможных признаков достаточно широк. В частности, при A = { z } A = { z } A={z}A=\{z\}A={z} он включает тождественную функцию f { z } ( x z ) = x z f { z } x z = x z f_({z})(x_(z))=x_(z)f_{\{z\}}\left(x_{z}\right)=x_{z}f{z}(xz)=xz. Так как f { Z } ∘ ξ { Z } = ξ { Z } f { Z } ∘ ξ { Z } = ξ { Z } f_({Z})@xi_({Z})=xi_({Z})f_{\{Z\}} \circ \xi_{\{Z\}}=\xi_{\{Z\}}f{Z}∘ξ{Z}=ξ{Z}, то каждая случайная величина ξ z ξ z xi_(z)\xi_{z}ξz является признаком. Его значениями служат амплитуды x z x z x_(z)x_{z}xz, соответствующие различным ω ∈ Ω ω ∈ Ω omega in Omega\omega \in \Omegaω∈Ω. В случае конечного подмножества A A AAA признаками являются сумма и произведение
f A ( x A ) = ∑ a ∈ A x a и f A ( x A ) = ∏ a ∈ A x a f A x A = ∑ a ∈ A   x a  и  f A x A = ∏ a ∈ A   x a f_(A)(x_(A))=sum_(a in A)x_(a)" и "f_(A)(x_(A))=prod_(a in A)x_(a)f_{A}\left(x_{A}\right)=\sum_{a \in A} x_{a} \text { и } f_{A}\left(x_{A}\right)=\prod_{a \in A} x_{a}fA(xA)=∑a∈Axa и fA(xA)=∏a∈Axa
а также отображение-константа f A ( x A ) = c , c ∈ R f A x A = c , c ∈ R f_(A)(x_(A))=c,c in Rf_{A}\left(x_{A}\right)=c, c \in RfA(xA)=c,c∈R. Также, используя (3.1.1), легко убедиться, что признаками являются приведенные ниже отображения
f A ( x A ) = 1 | A | ∑ z ∈ A x z и f A ( x A ) = | A | . f A x A = 1 | A | ∑ z ∈ A   x z  и  f A x A = | A | . f_(A)(x_(A))=(1)/(|A|)sum_(z in A)x_(z)" и "f_(A)(x_(A))=|A|.f_{A}\left(x_{A}\right)=\frac{1}{|A|} \sum_{z \in A} x_{z} \text { и } f_{A}\left(x_{A}\right)=|A| .fA(xA)=1|A|∑z∈Axz и fA(xA)=|A|.
В первом случае значением признака является среднее арифметическое значение амплитуд изображения x A x A x_(A)x_{A}xA. Во втором случае значение признака равняется количеству элементов подмножества A A AAA объекта, называемое обычно площадью его проекции. Она не зависит от амплитуд изображения x A x A x_(A)x_{A}xA. Такие признаки называются геометрическими.
Рассмотрим еще ряд часто используемых признаков, которые будут использоваться далее. Пусть B B BBB - подмножество на R R RRR, отображение I B : R → { 0 , 1 } I B : R → { 0 , 1 } I_(B):R rarr{0,1}I_{B}: R \rightarrow\{0,1\}IB:R→{0,1}, определяемое равенством
I B ( u ) = { 1 , u ∈ B 0 , u ∈ R ∖ B , I B ( u ) = 1 , u ∈ B 0 , u ∈ R ∖ B , I_(B)(u)={[1",",u in B],[0",",u in R\\B],:}I_{B}(u)=\left\{\begin{array}{ll} 1, & u \in B \\ 0, & u \in R \backslash B \end{array},\right.IB(u)={1,u∈B0,u∈R∖B,
называется его индикатором. Для любого борелевского подмножества C C CCC на R R RRR его прообразом I B − 1 ( C ) I B − 1 ( C ) I_(B)^(-1)(C)I_{B}^{-1}(C)IB−1(C) является одно из четырех борелевских подмножеств, указанных ниже
I B − 1 ( C ) = { u ∈ R : I B ( u ) ∈ C } = { B , 1 ∈ C R ∖ B , 0 ∈ C R , { 0 , 1 } ⊂ C ∅ , R ∖ { 0 , 1 } . I B − 1 ( C ) = u ∈ R : I B ( u ) ∈ C = B , 1 ∈ C R ∖ B , 0 ∈ C R , { 0 , 1 } ⊂ C ∅ , R ∖ { 0 , 1 } . I_(B)^(-1)(C)={u in R:I_(B)(u)in C}={[B","quad1in C],[R\\B","quad0in C],[R","quad{0","1}sub C],[O/","quad R\\{0","1}].:}I_{B}^{-1}(C)=\left\{u \in R: I_{B}(u) \in C\right\}=\left\{\begin{array}{c} B, \quad 1 \in C \\ R \backslash B, \quad 0 \in C \\ R, \quad\{0,1\} \subset C \\ \emptyset, \quad R \backslash\{0,1\} \end{array} .\right.IB−1(C)={u∈R:IB(u)∈C}={B,1∈CR∖B,0∈CR,{0,1}⊂C∅,R∖{0,1}.
Поэтому индикатор любого борелевского подмножества B B BBB на R R RRR является борелевским отображением.
Пусть ξ A − ξ A − xi_(A)-\xi_{A}-ξA− объект, x A − x A − x_(A)-x_{A}-xA− его изображение, y ∈ Y y ∈ Y y in Yy \in Yy∈Y - одно из возможных значений амплитуд, а n y − n y − n_(y)-n_{y}-ny− количество пикселей изображения x A x A x_(A)x_{A}xA, амплитуды которых равны y y yyy. В этом случае относительная частота n y / | A | n y / | A | n_(y)//|A|n_{y} /|A|ny/|A| амплитуды y y yyy на изображении x A x A x_(A)x_{A}xA также является признаком. В самом деле, каждая амплитуда является борелевским подмножеством на R R RRR, состоящим из одного элемента, а ее индикатор I { y } I { y } I_({y})I_{\{y\}}I{y} - борелевским отображением. Поэтому из (3.1.1) следует, что отображение f A f A f_(A)f_{A}fA, определяемое равенством
f A ( x A ) = 1 | A | ∑ a ∈ A I { y } ( x a ) = n y | A | , f A x A = 1 | A | ∑ a ∈ A   I { y } x a = n y | A | , f_(A)(x_(A))=(1)/(|A|)sum_(a in A)I_({y})(x_(a))=(n_(y))/(|A|),f_{A}\left(x_{A}\right)=\frac{1}{|A|} \sum_{a \in A} I_{\{y\}}\left(x_{a}\right)=\frac{n_{y}}{|A|},fA(xA)=1|A|∑a∈AI{y}(xa)=ny|A|,
является борелевским отображением или признаком объекта ξ A ξ A xi_(A)\xi_{A}ξA. Семейство ( n y / | A | ) y ∈ Y n y / | A | y ∈ Y (n_(y)//|A|)_(y in Y)\left(n_{y} /|A|\right)_{y \in Y}(ny/|A|)y∈Y относительных частот, построенное по изображению x A x A x_(A)x_{A}xA, является его гистограммой. Гистограмма служит важной характеристикой изображения. Очевидно, что при перестановке местами любых пикселей изображения гистограмма остается прежней. Поэтому одной и той же гистограмме могут соответствовать разные по содержанию изображения.
Рассмотрим менее очевидную ситуацию, которая возникает при сравнении объектов, проекциями которых являются квадраты B ( z , r ) B ( z , r ) B(z,r)B(z, r)B(z,r) на Z 2 Z 2 Z^(2)Z^{2}Z2. Предположим, что принятие некоторого решения зависит от результатов сравнения амплитуды x z x z x_(z)x_{z}xz центрального пикселя с амплитудами x t , t ∈ B ( z , r ) ∖ { z } x t , t ∈ B ( z , r ) ∖ { z } x_(t),t in B(z,r)\\{z}x_{t}, t \in B(z, r) \backslash\{z\}xt,t∈B(z,r)∖{z}, остальных пикселей. Поэтому в качестве значения признака объекта ξ B ( z , r ) ξ B ( z , r ) xi_(B(z,r))\xi_{B(z, r)}ξB(z,r) удобно рассматривать количество точек из множества B ( z , r ) ∖ { z } B ( z , r ) ∖ { z } B(z,r)\\{z}B(z, r) \backslash\{z\}B(z,r)∖{z}, для которых выполняется неравенство x z − x t > 0 x z − x t > 0 x_(z)-x_(t) > 0x_{z}-x_{t}>0xz−xt>0. Интервала ] 0 , + ∞ [ ] 0 , + ∞ [ ]0,+oo[] 0,+\infty[]0,+∞[ является борелевским подмножеством на R R RRR, а его индикатор I ] 0 , + ∞ I ] 0 , + ∞ I_(]0,+oo)I_{] 0,+\infty}I]0,+∞ - борелевским отображением вида R → { 0 , 1 } R → { 0 , 1 } R rarr{0,1}R \rightarrow\{0,1\}R→{0,1}. Из (3.1.1) следует, что отображение f B ( z , r ) f B ( z , r ) f_(B(z,r))f_{B(z, r)}fB(z,r), определяемое равенством
f B ( z , r ) ( x B ( z , r ) ) ) = ∑ t ∈ B ( z , r ) I ] 0 , + ∞ [ ( x z − x t ) , f B ( z , r ) x B ( z , r ) = ∑ t ∈ B ( z , r )   I ] 0 , + ∞ [ x z − x t , {:f_(B(z,r))(x_(B(z,r))))=sum_(t in B(z,r))I_(]0,+oo[)(x_(z)-x_(t)),\left.f_{B(z, r)}\left(x_{B(z, r)}\right)\right)=\sum_{t \in B(z, r)} I_{] 0,+\infty[ }\left(x_{z}-x_{t}\right),fB(z,r)(xB(z,r)))=∑t∈B(z,r)I]0,+∞[(xz−xt),
является борелевским, а значит признаком объекта ξ B ( z , r ) ξ B ( z , r ) xi_(B(z,r))\xi_{B(z, r)}ξB(z,r).
Рассмотренные примеры позволяют надеяться, что отображения f A f A f_(A)f_{A}fA, определяемые на множестве Y A Y A Y^(A)Y^{A}YA изображений объекта ξ A ξ A xi_(A)\xi_{A}ξA, при решении прикладных задач, в большинстве случаев окажутся действительно его признаками в смысле данного выше определения.
Довольно часто на множестве изображений объекта ξ A ξ A xi_(A)\xi_{A}ξA приходится определять одновременно не один, а несколько признаков. В качестве примеров можно указать среднее значение и среднеквадратическое отклонение
m A = 1 | A | ∑ a ∈ A x a и s A 2 = 1 | A | ∑ a ∈ A ( x a − m A ) 2 , m A = 1 | A | ∑ a ∈ A   x a  и  s A 2 = 1 | A | ∑ a ∈ A   x a − m A 2 , m_(A)=(1)/(|A|)sum_(a in A)x_(a)" и "s_(A)^(2)=(1)/(|A|)sum_(a in A)(x_(a)-m_(A))^(2),m_{A}=\frac{1}{|A|} \sum_{a \in A} x_{a} \text { и } s_{A}^{2}=\frac{1}{|A|} \sum_{a \in A}\left(x_{a}-m_{A}\right)^{2},mA=1|A|∑a∈Axa и sA2=1|A|∑a∈A(xa−mA)2,
а также гистограмму ( n y / | A | ) y ∈ Y n y / | A | y ∈ Y (n_(y)//|A|)_(y in Y)\left(n_{y} /|A|\right)_{y \in Y}(ny/|A|)y∈Y.

3.2 Форма объекта

Форма является важным дешифровочным признаком. Несмотря на ее широкое применение при визуальной классификации, общепризнанного определения этого понятия не существует. В настоящей работе в качестве формы ограниченной фигуры на плоскости предлагается использовать распределение двумерной случайной величины ( ξ , η ) ( ξ , η ) (xi,eta)(\xi, \eta)(ξ,η). Ее компонента ξ ξ xi\xiξ равняется числу хорд, вырезанных фигурой из проходящей через нее случайной прямой, а компонента η η eta\etaη - их суммарной длине. Очевидно, что выпуклая фигура будет всегда вырезать из прямой только одну хорду. Этот случай представлен на рисунке 3.3.1 (случайные прямые выделены цветом). Количество хорд, вырезаемых невыпуклой фигурой из прямой, зависит от ее формы. Иллюстрирующий эту ситуацию случай представлен на рисунке 3.3.2. Доказано, что определенная таким образом форма плоской фигуры является инвариантом группы движений, то есть не зависит от параллельного переноса фигуры на произвольный вектор и поворота на произвольный угол.
Рисунок 3.3.1 - Выпуклая проекция
Рисунок 3.3.2 - Невыпуклая проекция
Считается, что фигуры A A AAA и B B BBB имеют одинаковую форму, если распределения P A P A P_(A)P_{A}PA и P B P B P_(B)P_{B}PB случайных величин ( ξ A , η A ξ A , η A xi_(A),eta_(A)\xi_{A}, \eta_{A}ξA,ηA ) и ( ξ B , η B ξ B , η B xi_(B),eta_(B)\xi_{B}, \eta_{B}ξB,ηB ) совпадают. Сравнение распределений P A P A P_(A)P_{A}PA и P B P B P_(B)P_{B}PB (формы двух проекций A A AAA и B B BBB ) удобно выполнять с помощью методов математической статистики. В самом деле, пусть n A n A n_(A)n_{A}nA и n B n B n_(B)n_{B}nB - количество случайных прямых, вырезанных проекциями A A AAA и B B BBB соответственно, и пусть ( x j A , y j A ) 1 ≤ j ≤ n A x j A , y j A 1 ≤ j ≤ n A (x_(j)^(A),y_(j)^(A))_(1 <= j <= n_(A))\left(x_{j}^{A}, y_{j}^{A}\right)_{1 \leq j \leq n_{A}}(xjA,yjA)1≤j≤nA и ( x j B , y j B ) 1 ≤ j ≤ n B x j B , y j B 1 ≤ j ≤ n B (x_(j)^(B),y_(j)^(B))_(1 <= j <= n_(B))\left(x_{j}^{B}, y_{j}^{B}\right)_{1 \leq j \leq n_{B}}(xjB,yjB)1≤j≤nB - соответствующие им двумерные выборки. Решение о равенстве двух распределений принимается в зависимости от результата проверки гипотезы однородности. Эта гипотеза является предположением о том, что двумерные случайные величины ( ξ A , η A ξ A , η A xi_(A),eta_(A)\xi_{A}, \eta_{A}ξA,ηA ) и ( ξ B , η B ξ B , η B xi_(B),eta_(B)\xi_{B}, \eta_{B}ξB,ηB ) имеют одно и то же распределение. Принятие гипотезы при заданном уровне значимости α α alpha\alphaα означает, что распределения выборок совпадают, то есть обе проекции имеют одну и ту же форму. В противном случае (при отклонении гипотезы) принимается решение о том, что проекции имеют разную форму.
Очевидно, что по случайным причинам гипотеза может быть отклонена даже в случае совпадения формы сравниваемых фигур. Вероятность этого события равна α α alpha\alphaα.
Классификация по форме выполняется в несколько этапов. Вначале по изображению сцены определяется проекция объекта. На следующем этапе форма полученной проекции сравнивается с формой проекций объектов каждого класса. Эти проекции строятся по 3 d 3 d 3d3 d3d моделям соответствующих объектов. Необходимо иметь в виду, что ориентация (направление наблюдения) распознаваемого объекта и масштаб изображения могут оказаться неизвестными. В этом случае для каждого класса необходимо предварительно подготовить наборы проекций, соответствующих разным масштабам и ориентациям образующих его объектов. Такой набор будет называться далее описанием класса. Решение о классе предъявленного объекта принимается на третьем этапе. Объект относится к тому классу, для которого количество совпадений формы проекции, построенной по изображению сцены, с формой проекций, составляющих описание класса, оказалось максимальным.
Обсуждение проверки гипотезы однородности начнем со случая, когда проекции являются выпуклыми: каждая вырезает из случайной прямой только одну хорду. Пусть A A AAA и B B BBB - сравниваемые фигуры, а n A n A n_(A)n_{A}nA и n B n B n_(B)n_{B}nB - количество независимых случайные прямых, пересекающих A A AAA и B B BBB соответственно. Пусть l A = ( l A , k ) 1 ≤ k ≤ n A l A = l A , k 1 ≤ k ≤ n A l_(A)=(l_(A,k))_(1 <= k <= n_(A))l_{A}= \left(l_{A, k}\right)_{1 \leq k \leq n_{A}}lA=(lA,k)1≤k≤nA и l B = ( l B , k ) 1 ≤ k ≤ n B l B = l B , k 1 ≤ k ≤ n B l_(B)=(l_(B,k))_(1 <= k <= n_(B))l_{B}=\left(l_{B, k}\right)_{1 \leq k \leq n_{B}}lB=(lB,k)1≤k≤nB - выборки длин хорд, вырезанных из этих прямых фигурами A A AAA и B B BBB. Предположение о равенстве распределений P A P A P_(A)P_{A}PA и P B P B P_(B)P_{B}PB в математической статистике называется гипотезой однородности. Для ее проверки разобьем множество R R RRR вещественных чисел на s s sss интервалов. Пусть m A , j m A , j m_(A,j)m_{A, j}mA,j и m B , j m B , j m_(B,j)m_{B, j}mB,j - количество элементов выборок l A l A l_(A)l_{A}lA и l B l B l_(B)l_{B}lB соответственно, оказавшихся в j j jjj-ом интервале. Известно [68, с. 483], что при равенстве P A = P B P A = P B P_(A)=P_(B)P_{A}=P_{B}PA=PB распределение статистики X n A + n B 2 X n A + n B 2 X_(n_(A)+n_(B))^(2)X_{n_{A}+n_{B}}^{2}XnA+nB2 вида
X n A + n B 2 = n A n B ∑ 1 ≤ j ≤ s 1 m A , j + m B , j ( m A , j n A − m B , j n B ) 2 X n A + n B 2 = n A n B ∑ 1 ≤ j ≤ s   1 m A , j + m B , j m A , j n A − m B , j n B 2 X_(n_(A)+n_(B))^(2)=n_(A)n_(B)sum_(1 <= j <= s)(1)/(m_(A,j)+m_(B,j))((m_(A,j))/(n_(A))-(m_(B,j))/(n_(B)))^(2)X_{n_{A}+n_{B}}^{2}=n_{A} n_{B} \sum_{1 \leq j \leq s} \frac{1}{m_{A, j}+m_{B, j}}\left(\frac{m_{A, j}}{n_{A}}-\frac{m_{B, j}}{n_{B}}\right)^{2}XnA+nB2=nAnB∑1≤j≤s1mA,j+mB,j(mA,jnA−mB,jnB)2
стремиться к распределению χ 2 χ 2 chi^(2)\chi^{2}χ2 с ( s − 1 ) ( s − 1 ) (s-1)(s-1)(s−1) степенью при ( n A + n B ) → + ∞ n A + n B → + ∞ (n_(A)+n_(B))rarr+oo\left(n_{A}+n_{B}\right) \rightarrow+\infty(nA+nB)→+∞ свободы. Поэтому вероятность оказаться в интервале [ t , + ∞ [ [ t , + ∞ [ [t,+oo[[t,+\infty[[t,+∞[ для статистики X n A + n B 2 X n A + n B 2 X_(n_(A)+n_(B))^(2)X_{n_{A}+n_{B}}^{2}XnA+nB2 равняется приблизительно P ( χ 2 ≥ t ) P χ 2 ≥ t P(chi^(2) >= t)P\left(\chi^{2} \geq t\right)P(χ2≥t).
Сказанное позволяет свести сравнение фигур по форме к проверке гипотезы однородности. В самом деле, зададим малое положительное число α α alpha\alphaα (например, 0.01 , 0.005 0.01 , 0.005 0.01,0.0050.01,0.0050.01,0.005 или 0.001 ) и, решив уравнение P ( χ 2 ≥ t α ) = α P χ 2 ≥ t α = α P(chi^(2) >= t_(alpha))=alphaP\left(\chi^{2} \geq t_{\alpha}\right)=\alphaP(χ2≥tα)=α относи-
тельно t α t α t_(alpha)t_{\alpha}tα, построим критическую область [ t α , + ∞ [ t α , + ∞ [ [t_(alpha),+oo[:}\left[t_{\alpha},+\infty[\right.[tα,+∞[. Далее вычисляется значение статистики X n A + n B 2 X n A + n B 2 X_(n_(A)+n_(B))^(2)X_{n_{A}+n_{B}}^{2}XnA+nB2 и сравнивается с t α t α t_(alpha)t_{\alpha}tα. Неравенство X n A + n B 2 ≥ t α X n A + n B 2 ≥ t α X_(n_(A)+n_(B))^(2) >= t_(alpha)X_{n_{A}+n_{B}}^{2} \geq t_{\alpha}XnA+nB2≥tα означает, что произошло маловероятное (с вероятностью α α alpha\alphaα ) событие. В этом случае гипотеза о равенстве распределений P A P A P_(A)P_{A}PA и P B P B P_(B)P_{B}PB отвергается. В противном случае гипотеза принимается. Очевидно, что вероятность отвергнуть верную гипотезу равняется α α alpha\alphaα.
Наконец, перейдем к описанию формы невыпуклых фигур. Принципиальное отличие невыпуклой фигуры от выпуклой состоит в том, что она может вырезать из прямой нескольких отрезков, которые так же будут называться хордами. Следовательно, непосредственное применение предложенного выше определения формы для сравнения невыпуклых фигур не подходит. Поэтому каждой невыпуклой фигуре сопоставим не одну, а пару случайных величин. Первая случайная величина будет описывать число хорд, которые вырезает фигура из прямой линии. Вторая - общую длину всех хорд, вырезанных из прямой. Таким образом, форму невыпуклой фигуры можно рассматривать как распределение двумерной случайной величины. Две невыпуклые фигуры следует рассматривать как одинаковые по форме, если их распределения совпадают. Очевидно, что фигуры, получаемые друг из друга параллельным переносом или поворотом, будут иметь одну и ту же форму. Если применить определение формы невыпуклой фигуры для описания выпуклых фигур, то случайная величина, описывающая количество вырезанных хорд, будет принимать всегда (с вероятностью равной единице) значение 1. Это означает, что определение формы выпуклой фигуры является частным случаем определения формы невыпуклых фигур. Таким образом, для сравнения двух фигур по форме достаточно получить для каждой из них двумерную выборку и проверить гипотезу однородности...

3.3 Задача классификации объектов

Классификацией принято называть задачу об определении принадлежности объектов некоторого множества к одному из заранее определенных и непересекающихся подмножеств, называемых классами. Для ее решения используются характерные свойства (признаки) объектов. При этом предполагается, что сходство (измеряемое тем или иным способом) объектов, принадлежащих одному классу, должно быть выше, чем у объектов, принадлежащих разным классам. При числе классов, равным двум, классификация обычно называется обнаружением, а при числе классов равным числу объектов - идентификацией.
Введем терминологию, принятую в данной области исследований. Пусть Ω Ω Omega\OmegaΩ - множество объектов, разделенное на K K KKK непересекающихся классов ( Ω j ) 1 ≤ j ≤ K Ω j 1 ≤ j ≤ K (Omega_(j))_(1 <= j <= K)\left(\Omega_{j}\right)_{1 \leq j \leq K}(Ωj)1≤j≤K. Каждому объекту ω ∈ Ω ω ∈ Ω omega in Omega\omega \in \Omegaω∈Ω соответствует v v vvv-мерный вектор x = ( x 1 , … , x v ) x = x 1 , … , x v x=(x_(1),dots,x_(v))x= \left(x_{1}, \ldots, x_{v}\right)x=(x1,…,xv) с вещественными координатами, который называется вектором признаков объекта ω ω omega\omegaω, а его координаты x j x j x_(j)x_{j}xj - признаками. Решение задачи классификации заключается в задании на множестве R v R v R^(v)R^{v}Rv, состоящем из всех векторов признаков, отображения h h hhh, называемого решающим правилом, которое каждому вектору признаков x ∈ R v x ∈ R v x inR^(v)x \in R^{v}x∈Rv ставит в соответствие номер h ( x ) h ( x ) h(x)h(x)h(x) класса, 1 ≤ h ( x ) ≤ K 1 ≤ h ( x ) ≤ K 1 <= h(x) <= K1 \leq h(x) \leq K1≤h(x)≤K, к которому следует отнести объект с признаком x x xxx. Классификация объекта ω ω omega\omegaω из j j jjj-ого класса Ω j Ω j Omega_(j)\Omega_{j}Ωj считается правильной, если h ( x ) = j h ( x ) = j h(x)=jh(x)=jh(x)=j. В противном случае классификация считается ошибочной.
Совокупность объектов, поступающих на классификацию, принято называть смесью. Смесь считается заданной, если выполняются два условия. Вопервых, для каждого класса Ω j Ω j Omega_(j)\Omega_{j}Ωj известна вероятность P ( Ω j ) P Ω j P(Omega_(j))P\left(\Omega_{j}\right)P(Ωj) появления принадлежащих ему объектов в смеси. Она называется априорной вероятностью класса. Во-вторых, для каждого класса Ω j Ω j Omega_(j)\Omega_{j}Ωj известно распределение (например плотность p j p j p_(j)p_{j}pj ) признаков для образующих его объектов. В качестве количественной оценки эффективности классификации Байес предложил использовать вероятность правильной классификации объектов смеси (или вероятность ошибки классификации). Он же указал вид решающего правила, для которого эта вероятность является максимальной. Пусть x x xxx - вектор признаков объекта ω ω omega\omegaω. В соответствии с теоремой Байеса объект ω ω omega\omegaω следует отнести к классу Ω k Ω k Omega_(k)\Omega_{k}Ωk, для которого неравенство
P ( Ω k ) p k ( x ) ≥ P ( Ω j ) p j ( x ) P Ω k p k ( x ) ≥ P Ω j p j ( x ) P(Omega_(k))p_(k)(x) >= P(Omega_(j))p_(j)(x)P\left(\Omega_{k}\right) p_{k}(x) \geq P\left(\Omega_{j}\right) p_{j}(x)P(Ωk)pk(x)≥P(Ωj)pj(x)
выполняется при любых j , 1 ≤ j ≤ K j , 1 ≤ j ≤ K j,1 <= j <= Kj, 1 \leq j \leq Kj,1≤j≤K. Такое решающее правило стало называться оптимальным.
При заданной смеси и выбранном решающем правиле можно вычислить вероятность e ( h ) e ( h ) e(h)e(h)e(h) правильной классификации объектов, образующих смесь. В случае известных плотностей она принимает вид
e ( h ) = ∑ j ∈ K P ( Ω j ) ∫ h − 1 ( { j } ) p j ( x ) d x e ( h ) = ∑ j ∈ K   P Ω j ∫ h − 1 ( { j } )   p j ( x ) d x e(h)=sum_(j in K)P(Omega_(j))int_(h^(-1)({j}))p_(j)(x)dxe(h)=\sum_{j \in K} P\left(\Omega_{j}\right) \int_{h^{-1}(\{j\})} p_{j}(x) d xe(h)=∑j∈KP(Ωj)∫h−1({j})pj(x)dx
Если признаки являются дискретными случайными величинами, то
e ( h ) = ∑ j ∈ K P ( Ω j ) ∑ x ∈ h − 1 ( { j } ) ∩ Q j P j ( { x } ) . e ( h ) = ∑ j ∈ K   P Ω j ∑ x ∈ h − 1 ( { j } ) ∩ Q j   P j ( { x } ) . e(h)=sum_(j in K)P(Omega_(j))sum_(x inh^(-1)({j})nnQ_(j))P_(j)({x}).e(h)=\sum_{j \in K} P\left(\Omega_{j}\right) \sum_{x \in h^{-1}(\{j\}) \cap Q_{j}} P_{j}(\{x\}) .e(h)=∑j∈KP(Ωj)∑x∈h−1({j})∩QjPj({x}).
К сожалению, при решении прикладных задач сведения об априорных вероятностях классов и распределениях признаков в них часто отсутствуют. Поэтому применить оптимальное правило не удается.
На рисунках 3.3.1 и 3.3.2 приведены два примера геометрической интерпретации теоремы Байеса для случая двух классов и одного признака. Из-за отсутствия у текстового редактора греческого алфавита на рисунках вместо буквы «Ω» в обозначениях классов используется буква «О».
Рисунок 3.3.1
Рисунок 3.3.2
При значении признака x < x 0 x < x 0 x < x_(0)x<x_{0}x<x0 выполняется неравенство P ( Ω 1 ) p 1 ( x ) > P ( Ω 2 ) p 2 ( x ) P Ω 1 p 1 ( x ) > P Ω 2 p 2 ( x ) P(Omega_(1))p_(1)(x) > P(Omega_(2))p_(2)(x)P\left(\Omega_{1}\right) p_{1}(x)> P\left(\Omega_{2}\right) p_{2}(x)P(Ω1)p1(x)>P(Ω2)p2(x). В соответствии с теоремой Байеса решение принимается в пользу первого класса. Поэтому все объекты второго класса, у которых x < x 0 x < x 0 x < x_(0)x<x_{0}x<x0, классифицируются неверно. Для x > x 0 x > x 0 x > x_(0)x>x_{0}x>x0 имеет место противоположное неравенство P ( Ω 1 ) p 1 ( x ) < P ( Ω 2 ) p 2 ( x ) P Ω 1 p 1 ( x ) < P Ω 2 p 2 ( x ) P(Omega_(1))p_(1)(x) < P(Omega_(2))p_(2)(x)P\left(\Omega_{1}\right) p_{1}(x)<P\left(\Omega_{2}\right) p_{2}(x)P(Ω1)p1(x)<P(Ω2)p2(x). Поэтому решение принимается в пользу второго класса. Следовательно все объекты первого класса, у которых x > x 0 x > x 0 x > x_(0)x>x_{0}x>x0, классифицируются неверно. При x = x 0 x = x 0 x=x_(0)x=x_{0}x=x0 имеет место равенство P ( Ω 1 ) p 1 ( x ) = P Ω 1 p 1 ( x ) = P(Omega_(1))p_(1)(x)=P\left(\Omega_{1}\right) p_{1}(x)=P(Ω1)p1(x)=
P ( Ω 2 ) p 2 ( x ) P Ω 2 p 2 ( x ) P(Omega_(2))p_(2)(x)P\left(\Omega_{2}\right) p_{2}(x)P(Ω2)p2(x). Поэтому объект можно отнести к любому классу. Из сравнения рисунков следует, что число неверных классификаций в случае, представленном на рисунке 3.3.2, значительно больше, чем в случае с рисунка 3.3.1.

Глава 4 СЕГМЕНТАЦИЯ ИЗОБРАЖЕНИЙ

Форма проекции объекта на плоскость перпендикулярную направлению наблюдения является важным демаскирующим признаком. Очевидно, что площадь, периметр и другие свойства проекции также, как и ее форма, могут использоваться в качестве признаков объекта, которые называются геометрическими. Для того, чтобы ими воспользоваться, требуется построить проекцию объекта по изображению сцены. Задача, состоящая в определении проекций объектов, присутствующих на сцене, по ее изображению будет называться далее сегментацией. Результат ее решения можно наглядно представить в виде специализированного изображения (карты). На ней пиксели каждой проекции имеют одну и ту же амплитуду, называемую псевдоцветом.
Довольно часто изображения используются для выявления на сцене объектов определенного типа. Решением такой задачи, называемой обнаружением объектов, является набор координат всех обнаруженных объектов. При этом в качестве координат объекта могут рассматриваться, например, координаты центра прямоугольника со сторонами параллельными сторонам изображения, описанного вокруг его проекции. При отсутствии сведений о местонахождении объектов приходится проводить обнаружение в каждом месте сцены, где они могут находится. Если известен масштаб изображения, то на нем можно указать семейство квадратных фрагментов, удовлетворяющих двум свойствам. Во-первых, для любого объекта, присутствующего на сцене, существует хотя бы один фрагмент, содержащий его проекцию. Во-вторых, все точки проекции являются внутренними точками квадратного фрагмента. Фрагменты с такими свойствами будут называться далее зонами интереса. Из сказанного следует, что обнаружение присутствующих на сцене объектов сводится к заданию на изображении семейства квадратных фрагментов и решению задачи обнаружения в каждом из них. Пиксели зоны интереса, не принадлежащие объекту, часто называются его окружением или фоном. Он может оказаться простым фрагментом однородного случайного поля или сложным. В последнем случае он состоит из фрагментов разных однородных случайных полей.

4.1 Зоны интереса

Квадратом на Z 2 Z 2 Z^(2)Z^{2}Z2 с верхней левой вершиной в точке c = ( c 1 , c 2 ) ∈ Z 2 c = c 1 , c 2 ∈ Z 2 c=(c_(1),c_(2))inZ^(2)c=\left(c_{1}, c_{2}\right) \in Z^{2}c=(c1,c2)∈Z2 и стороной из l l lll пикселей назовем подмножество Q ( c ) ⊂ Z 2 Q ( c ) ⊂ Z 2 Q(c)subZ^(2)Q(c) \subset Z^{2}Q(c)⊂Z2, определяемое равенством
Q ( c ) = { ( z 1 , z 2 ) ∈ Z 2 : c 1 ≤ z 1 < c 1 + l , c 2 ≤ z 2 < c 2 + l } Q ( c ) = z 1 , z 2 ∈ Z 2 : c 1 ≤ z 1 < c 1 + l , c 2 ≤ z 2 < c 2 + l Q(c)={(z_(1),z_(2))inZ^(2):c_(1) <= z_(1) < c_(1)+l,c_(2) <= z_(2) < c_(2)+l}Q(c)=\left\{\left(z_{1}, z_{2}\right) \in Z^{2}: c_{1} \leq z_{1}<c_{1}+l, c_{2} \leq z_{2}<c_{2}+l\right\}Q(c)={(z1,z2)∈Z2:c1≤z1<c1+l,c2≤z2<c2+l}
Вершина квадрата может не указываться в тех случаях, когда это не приводит
к неопределенности.
Пусть Q Q QQQ - квадрат. Семейство ξ Q = ( ξ z ) z ∈ Q ξ Q = ξ z z ∈ Q xi_(Q)=(xi_(z))_(z in Q)\xi_{Q}=\left(\xi_{z}\right)_{z \in Q}ξQ=(ξz)z∈Q случайных величин будет называться зоной интереса объекта ξ A ξ A xi_(A)\xi_{A}ξA, если, выполняются два следующих условия. Во-первых, проекция A A AAA объекта состоит только из внутренних точек квадрата Q : A ⊂ Q ∖ F r Q Q : A ⊂ Q ∖ F r Q Q:A sub Q\\Fr_(Q)Q: A \subset Q \backslash F r_{Q}Q:A⊂Q∖FrQ. Во-вторых, среди остальных пикселей ξ Q ∖ A ξ Q ∖ A xi_(Q\\A)\xi_{Q \backslash A}ξQ∖A зоны интереса отсутствуют пиксели, принадлежащие другим объектам того же типа, что и ξ A ξ A xi_(A)\xi_{A}ξA. Совокупность ξ Q ∖ A ξ Q ∖ A xi_(Q\\A)\xi_{Q \backslash A}ξQ∖A остальных пикселей зоны интереса будет называться окружением объекта ξ A ξ A xi_(A)\xi_{A}ξA или его фоном.
Пусть ξ A ξ A xi_(A)\xi_{A}ξA - объект, число D ( A ) D ( A ) D(A)D(A)D(A), определяемое равенством
D ( A ) = max a ∈ A , b ∈ A d ( a , b ) D ( A ) = max a ∈ A , b ∈ A   d ( a , b ) D(A)=max_(a in A,b in A)d(a,b)D(A)=\max _{a \in A, b \in A} d(a, b)D(A)=maxa∈A,b∈Ad(a,b)
назовем диаметром объекта ξ A ξ A xi_(A)\xi_{A}ξA. Вместо D ( A ) D ( A ) D(A)D(A)D(A) может использоваться короткое обозначение D D DDD, если это не приводит к неопределенности. Если ξ Q ξ Q xi_(Q)\xi_{Q}ξQ - зона интереса объекта ξ A ξ A xi_(A)\xi_{A}ξA с диаметром D D DDD, то для стороны l l lll квадрата Q Q QQQ должно выполняться неравенство l ≥ D + 2 l ≥ D + 2 l >= D+2l \geq D+2l≥D+2. В самом деле, если ( c 1 , c 2 c 1 , c 2 c_(1),c_(2)c_{1}, c_{2}c1,c2 ) - координаты левой верхней вершины квадрата, то ( c 1 + l , c 2 c 1 + l , c 2 c_(1)+l,c_(2)c_{1}+l, c_{2}c1+l,c2 ) - координаты его правой верхней вершины. Поэтому для любых точек a a aaa и b b bbb проекции A A AAA должно выполняться неравенство d ( a , b ) ≤ D d ( a , b ) ≤ D d(a,b) <= Dd(a, b) \leq Dd(a,b)≤D. Поскольку A A AAA состоит из внутренних точек, то l ≥ D + 2 l ≥ D + 2 l >= D+2l \geq D+2l≥D+2. Очевидно, что у объекта может быть несколько зон интереса.
В качестве обоснования целесообразности введения понятия зоны интереса приведем следующие соображения, которые будут использоваться далее. Пусть x Q = ( x z ) z ∈ Q x Q = x z z ∈ Q x_(Q)=(x_(z))_(z in Q)x_{Q}=\left(x_{z}\right)_{z \in Q}xQ=(xz)z∈Q - изображение зоны интереса ξ Q ξ Q xi_(Q)\xi_{Q}ξQ объекта ξ A ξ A xi_(A)\xi_{A}ξA. Из ее определения следует, что пиксели ξ F r ( Q ) ξ F r ( Q ) xi_(Fr(Q))\xi_{F r(Q)}ξFr(Q) границы зоны интереса не принадлежат самому объекту ξ A ξ A xi_(A)\xi_{A}ξA. Поэтому изображение ( x Z ) Z ∈ F r ( Q ) x Z Z ∈ F r ( Q ) (x_(Z))_(Z in Fr(Q))\left(x_{Z}\right)_{Z \in F r(Q)}(xZ)Z∈Fr(Q) границы позволяют получить сведения о свойствах амплитуд пикселей из окружения объекта. Эти сведения могут использоваться для классификации по амплитуде внутренних пикселей зоны интереса на два класса с условными названиями «Объект» и «Фон». Для этого амплитуда x z x z x_(z)x_{z}xz каждого внутреннего пикселя z ∈ Q ∖ F r Q z ∈ Q ∖ F r Q z in Q\\Fr_(Q)z \in Q \backslash F r_{Q}z∈Q∖FrQ зоны интереса сравнивается тем или иным способом с амплитудами ( x z ) z ∈ F r ( Q ) x z z ∈ F r ( Q ) (x_(z))_(z in Fr(Q))\left(x_{z}\right)_{z \in F r(Q)}(xz)z∈Fr(Q) пикселей границы. В случае сходства пиксель относится к классу Фон. В противном случае пиксель относится к классу Объект. Полученная в результате сегментации проекция объекта используется далее для его классификации. Как правило, в зоне интереса присутствуют пиксели с одинаковой амплитудой, но принадлежащие объекту и фону. Их появление приводит к неизбежным ошибкам сегментации. Для снижения числа ошибок при сегментации следует использовать дополнительные признаки кроме амплитудных. В приводимой ниже теореме перечисляются требования к квадратам, гарантирующие выполнение первого условия, сформулированного в определении зоны интереса.
(4.1.1) Пусть ξ A ξ A xi_(A)\xi_{A}ξA - объект, D D DDD - его диаметр, l l lll - целое число такое, что l ≥ ( D + 2 ) l ≥ ( D + 2 ) l >= (D+2)l \geq (D+2)l≥(D+2), и Δ Δ Delta\DeltaΔ - целое число, удовлетворяющий неравенству 0 < Δ < ( l − D ) 0 < Δ < ( l − D ) 0 < Delta < (l-D)0<\Delta<(l-D)0<Δ<(l−D). Тогда среди всех квадратов со стороной l l lll и вершинами в точках ( m Δ , n Δ ) , m ∈ Z ( m Δ , n Δ ) , m ∈ Z (m Delta,n Delta),m in Z(m \Delta, n \Delta), m \in Z(mΔ,nΔ),m∈Z
и n ∈ Z n ∈ Z n in Zn \in Zn∈Z, найдется хотя бы один такой квадрат Q Q QQQ, что все точки проекции A A AAA окажутся его внутренними точками: A ⊂ Q ∖ E r Q A ⊂ Q ∖ E r Q A sub Q\\Er_(Q)A \subset Q \backslash E r_{Q}A⊂Q∖ErQ.
Доказательство. В частном случае, когда l = D + 2 l = D + 2 l=D+2l=D+2l=D+2, а Δ = 1 Δ = 1 Delta=1\Delta=1Δ=1, утверждение теоремы очевидно. Рассмотрим общий случай. Пусть a 1 ∈ Z 2 a 1 ∈ Z 2 a_(1)inZ^(2)a_{1} \in Z^{2}a1∈Z2 - горизонтальная координата самого левого пикселя и a 2 ∈ Z 2 a 2 ∈ Z 2 a_(2)inZ^(2)a_{2} \in Z^{2}a2∈Z2 - вертикальная координата самого верхнего пикселя проекции A A AAA. По условию теоремы Δ > 0 Δ > 0 Delta > 0\Delta>0Δ>0. Поэтому существуют целые числа q 1 q 1 q_(1)q_{1}q1 и q 2 q 2 q_(2)q_{2}q2 такие, что выполняются неравенства
q 1 < a 1 ≤ q 1 + Δ и q 2 < a 2 ≤ q 2 + Δ . q 1 < a 1 ≤ q 1 + Δ  и  q 2 < a 2 ≤ q 2 + Δ .  q_(1) < a_(1) <= q_(1)+Delta" и "q_(2) < a_(2) <= q_(2)+Delta". "q_{1}<a_{1} \leq q_{1}+\Delta \text { и } q_{2}<a_{2} \leq q_{2}+\Delta \text {. }q1<a1≤q1+Δ и q2<a2≤q2+Δ. 
Пусть b 1 ∈ Z 2 b 1 ∈ Z 2 b_(1)inZ^(2)b_{1} \in Z^{2}b1∈Z2 - горизонтальная координата самого правого пикселя, а b 2 ∈ Z 2 b 2 ∈ Z 2 b_(2)inZ^(2)b_{2} \in Z^{2}b2∈Z2 - вертикальная координата самого нижнего пикселя проекции A A AAA. Так как D D DDD - диаметр, то b 1 − a 1 ≤ D b 1 − a 1 ≤ D b_(1)-a_(1) <= Db_{1}-a_{1} \leq Db1−a1≤D и b 2 − a 2 ≤ D b 2 − a 2 ≤ D b_(2)-a_(2) <= Db_{2}-a_{2} \leq Db2−a2≤D. Поэтому
b 1 ≤ a 1 + D , a b 2 ≤ a 2 + D b 1 ≤ a 1 + D ,  a  b 2 ≤ a 2 + D b_(1) <= a_(1)+D," a "b_(2) <= a_(2)+Db_{1} \leq a_{1}+D, \text { a } b_{2} \leq a_{2}+Db1≤a1+D, a b2≤a2+D
Используя выше полученные оценки для a 1 a 1 a_(1)a_{1}a1 и a 2 a 2 a_(2)a_{2}a2, имеем
b 1 ≤ q 1 + Δ + D и b 2 ≤ q 2 + Δ + D . b 1 ≤ q 1 + Δ + D  и  b 2 ≤ q 2 + Δ + D . b_(1) <= q_(1)+Delta+D" и "b_(2) <= q_(2)+Delta+D.b_{1} \leq q_{1}+\Delta+D \text { и } b_{2} \leq q_{2}+\Delta+D .b1≤q1+Δ+D и b2≤q2+Δ+D.
По предположению теоремы Δ < ( l − D ) Δ < ( l − D ) Delta < (l-D)\Delta<(l-D)Δ<(l−D). Следовательно,
b 1 < q 1 + l и b 2 < q 2 + l . b 1 < q 1 + l  и  b 2 < q 2 + l . b_(1) < q_(1)+l" и "b_(2) < q_(2)+l.b_{1}<q_{1}+l \text { и } b_{2}<q_{2}+l .b1<q1+l и b2<q2+l.
Пусть Q ( q ) Q ( q ) Q(q)Q(q)Q(q) - квадрат со стороной l l lll и вершиной в точке q = ( q 1 , q 2 ) q = q 1 , q 2 q=(q_(1),q_(2))q=\left(q_{1}, q_{2}\right)q=(q1,q2). Точки a = ( a 1 , a 2 ) a = a 1 , a 2 a=(a_(1),a_(2))a=\left(a_{1}, a_{2}\right)a=(a1,a2) и b = ( b 1 , b 2 ) b = b 1 , b 2 b=(b_(1),b_(2))b=\left(b_{1}, b_{2}\right)b=(b1,b2) являются его внутренними точками по построению. Легко проверить, что проекция A A AAA принадлежит квадрату вершиной a a aaa и стороной max { ( b 2 − a 2 ) , ( b 1 − a 1 ) } max b 2 − a 2 , b 1 − a 1 max{(b_(2)-a_(2)),(b_(1)-a_(1))}\max \left\{\left(b_{2}-a_{2}\right),\left(b_{1}-a_{1}\right)\right\}max{(b2−a2),(b1−a1)}, состоящего из внутренних точек Q Q QQQ. Таким образом, теорема доказана.
Второе условие из определения зоны интереса запрещает присутствие в ней пикселей других объектов. Очевидно, что оно выполняется, если расстояние между объектами превышает некоторое минимальное значение.
Пусть ξ Q ξ Q xi_(Q)\xi_{Q}ξQ - зона интереса объекта ξ A ξ A xi_(A)\xi_{A}ξA, в соответствии со вторым условием ее определения в ξ Q ∖ A ξ Q ∖ A xi_(Q\\A)\xi_{Q \backslash A}ξQ∖A объекта должны отсутствовать пиксели других объектов того же типа. Это ...
Теорема 4.1.2. Пусть D D DDD - диаметр объекта ξ A , d , d > 1 , − ξ A , d , d > 1 , − xi_(A),d,d > 1,-\xi_{A}, d, d>1,-ξA,d,d>1,− минимальное расстояние между такими объектами, а Q Q QQQ - квадрат со стороной l l lll, такой, что A ⊂ Q ∖ E r ( Q ) A ⊂ Q ∖ E r ( Q ) A sub Q\\Er(Q)A \subset Q \backslash E r(Q)A⊂Q∖Er(Q). Если l ≤ ( D + 2 d ) l ≤ ( D + 2 d ) l <= (D+2d)l \leq(D+2 d)l≤(D+2d), то Q Q QQQ является зоной интереса для ξ A ξ A xi_(A)\xi_{A}ξA.
Доказательство. Существует квадрат со стороной D D DDD, содержащий проекцию A A AAA.
Это условие выполняется, если расстояние между объектами, которые требуется обнаружить, больше ( l 2 ) / 2 ( l 2 ) / 2 (lsqrt2)//2(l \sqrt{2}) / 2(l2)/2 пикселей. В этом случае обнаружение достаточно провести только среди всех квадратов со стороной l l lll и вершинами
в точках ( m Δ , n Δ ) , m ∈ Z ( m Δ , n Δ ) , m ∈ Z (m Delta,n Delta),m in Z(m \Delta, n \Delta), m \in Z(mΔ,nΔ),m∈Z и Z ∈ R Z ∈ R Z in RZ \in RZ∈R.
Пусть h h hhh и w w www - натуральные числа, C C CCC - прямоугольник на Z 2 Z 2 Z^(2)Z^{2}Z2 с высотой h h hhh и шириной w w www, определяемый равенством
C = { z = ( z 1 , z 2 ) ∈ Z 2 : 0 ≤ z 1 < h , 0 ≤ z 2 < w } , C = z = z 1 , z 2 ∈ Z 2 : 0 ≤ z 1 < h , 0 ≤ z 2 < w , C={z=(z_(1),z_(2))inZ^(2):0 <= z_(1) < h,0 <= z_(2) < w},C=\left\{z=\left(z_{1}, z_{2}\right) \in Z^{2}: 0 \leq z_{1}<h, 0 \leq z_{2}<w\right\},C={z=(z1,z2)∈Z2:0≤z1<h,0≤z2<w},
а x C x C x_(C)x_{C}xC - изображение из h h hhh строк и w w www столбцов некоторого участка сцены. При отсутствии сведений о местонахождении и ориентации объектов на сцене приходится проводить их обнаружение во всех местах сцены, где они могут находится, то есть выполнять поиск. Для этого по известному диаметру D D DDD объектов выбирается сторона l ≥ ( D + 2 ) l ≥ ( D + 2 ) l >= (D+2)l \geq(D+2)l≥(D+2) зоны интереса, величина Δ < ( l − D ) Δ < ( l − D ) Delta < (l-D)\Delta<(l-D)Δ<(l−D) и проводится обнаружение только в тех квадратах с вершинами ( m Δ , n Δ ) ∈ C ( m Δ , n Δ ) ∈ C (m Delta,n Delta)in C(m \Delta, n \Delta) \in C(mΔ,nΔ)∈C и стороной l l lll, которые принадлежат C C CCC. Очевидно, что координаты m m mmm и n n nnn их вершин должны удовлетворять следующим неравенствам
0 ≤ m Δ ≤ ( h − l ) Δ и 0 ≤ n Δ ≤ ( w − l ) Δ . 0 ≤ m Δ ≤ ( h − l ) Δ  и  0 ≤ n Δ ≤ ( w − l ) Δ .  0 <= m Delta <= (h-l)Delta" и "0 <= n Delta <= (w-l)Delta". "0 \leq m \Delta \leq(h-l) \Delta \text { и } 0 \leq n \Delta \leq(w-l) \Delta \text {. }0≤mΔ≤(h−l)Δ и 0≤nΔ≤(w−l)Δ. 
Пусть [ x ] [ x ] [x][x][x] - целая часть числа x x xxx, тогда количество N N NNN таких квадратов равняется
N = ( [ h − l Δ ] + 1 ) ( [ w − l Δ ] + 1 ) . N = h − l Δ + 1 w − l Δ + 1 . N=([(h-l)/(Delta)]+1)([(w-l)/(Delta)]+1).N=\left(\left[\frac{h-l}{\Delta}\right]+1\right)\left(\left[\frac{w-l}{\Delta}\right]+1\right) .N=([h−lΔ]+1)([w−lΔ]+1).
С увеличением Δ Δ Delta\DeltaΔ количество квадратов убывает со скоростью ( 1 / Δ ) 2 ( 1 / Δ ) 2 (1//Delta)^(2)(1 / \Delta)^{2}(1/Δ)2. С другой стороны, рост l l lll также уменьшает N N NNN и одновременно приводит к увеличению окрестности проекции. Это может усложнить сегментацию увеличенной зоны интереса. Если в ходе увеличения размеров в квадрате ξ A ξ A xi_(A)\xi_{A}ξA появятся пиксели других объектов такого же типа, то он (квадрат) перестанет быть зоной интереса.

4.2 Сегментация простых зон интереса

Далее будут рассматриваться зоны интереса двух типов. Зона интереса ξ Q ξ Q xi_(Q)\xi_{Q}ξQ будет называться простой, если находящийся в ней объект ξ A ξ A xi_(A)\xi_{A}ξA и его окрестность ξ Q ∖ A ξ Q ∖ A xi_(Q\\A)\xi_{Q \backslash A}ξQ∖A являются фрагментами разных однородных случайных полей. При этом случайное поле со средним значением m A m A m_(A)m_{A}mA и корреляционной функцией r A r A r_(A)r_{A}rA описывает свойства объекта, а случайное поле со средним значением m Q ∖ A m Q ∖ A m_(Q\\A)m_{Q \backslash A}mQ∖A и корреляционной функцией r Q ∖ A r Q ∖ A r_(Q\\A)r_{Q \backslash A}rQ∖A описывает свойства его окрестности. Признаком простой зоны интереса служит присутствие на гистограмме амплитуд зоны интереса, построенной по ее изображению, как правило, двух явно выраженных локальных максимумов, соответствующих объекту и фону. В качестве иллюстрации сказанного на рисунке 4.2.1 приведен фрагмент реального изображения с выбранной на нем зоной интереса, а на рисунке 4.2.2 - соответствующая ей гистограмма. Важно отметить, что фактическое количество локальных максимумов на гистограмме намного больше двух. Все локальные максимумы, кроме двух, вызваны случайными изменениями амплитуд и поэтому будут называться ложными. Локальные максимумы, соответствующие объекту (значение амплитуды 96) и фону (значение амплитуды 192), будут называться реальными максимумами. Вопрос о том, как отличать ложные локальные максимумы от реальных будет подробно обсуждаться далее в п.4.4.
Рисунок 4.2.1 - Зона интереса
Рисунок 4.2.2 - Гистограмма зоны интереса
Пусть x Q x Q x_(Q)x_{Q}xQ - изображение простой зоны интереса ξ Q ξ Q xi_(Q)\xi_{Q}ξQ с объектом ξ A ξ A xi_(A)\xi_{A}ξA и его окрестности ξ Q ∖ A ξ Q ∖ A xi_(Q\\A)\xi_{Q \backslash A}ξQ∖A. Ее сегментация заключается в разделении (классификации) пикселей, образующих ξ Q ξ Q xi_(Q)\xi_{Q}ξQ, на два класса с условными названиями «Объект» и «Фон» по ее изображению x Q x Q x_(Q)x_{Q}xQ. Как правило, информация о средних значениях m A m A m_(A)m_{A}mA и m Q ∖ A m Q ∖ A m_(Q\\A)m_{Q \backslash A}mQ∖A объекта и фона, а также их корреляционных функциях r A r A r_(A)r_{A}rA и r Q ∖ A r Q ∖ A r_(Q\\A)r_{Q \backslash A}rQ∖A отсутствует. Однако, из определения зоны интереса следует, что пиксели, образующие ее границу ξ F r ( Q ) ξ F r ( Q ) xi_(Fr(Q))\xi_{F r(Q)}ξFr(Q), принадлежат фону. Поэтому изображение x F r ( Q ) x F r ( Q ) x_(Fr(Q))x_{F r(Q)}xFr(Q) границы может использоваться для вычисления оценок x ¯ Q ∖ A x ¯ Q ∖ A bar(x)_(Q\\A)\bar{x}_{Q \backslash A}x¯Q∖A и s Q ∖ A s Q ∖ A s_(Q\\A)s_{Q \backslash A}sQ∖A неизвестных среднего значения m Q ∖ A m Q ∖ A m_(Q\\A)m_{Q \backslash A}mQ∖A и среднеквадратического отклонения σ Q ∖ A σ Q ∖ A sigma_(Q\\A)\sigma_{Q \backslash A}σQ∖A фона соответственно:
x ¯ Q ∖ A = 1 | F r ( Q ) | ∑ z ∈ F r ( Q ) x z , s Q ∖ A = ( 1 | F r ( Q ) | ∑ z ∈ F r ( Q ) ( x z − x ¯ Q ∖ A ) 2 ) 1 / 2 x ¯ Q ∖ A = 1 | F r ( Q ) | ∑ z ∈ F r ( Q )   x z , s Q ∖ A = 1 | F r ( Q ) | ∑ z ∈ F r ( Q )   x z − x ¯ Q ∖ A 2 1 / 2 bar(x)_(Q\\A)=(1)/(|Fr(Q)|)sum_(z in Fr(Q))x_(z),quads_(Q\\A)=((1)/(|Fr(Q)|)sum_(z in Fr(Q))(x_(z)- bar(x)_(Q\\A))^(2))^(1//2)\bar{x}_{Q \backslash A}=\frac{1}{|F r(Q)|} \sum_{z \in F r(Q)} x_{z}, \quad s_{Q \backslash A}=\left(\frac{1}{|F r(Q)|} \sum_{z \in F r(Q)}\left(x_{z}-\bar{x}_{Q \backslash A}\right)^{2}\right)^{1 / 2}x¯Q∖A=1|Fr(Q)|∑z∈Fr(Q)xz,sQ∖A=(1|Fr(Q)|∑z∈Fr(Q)(xz−x¯Q∖A)2)1/2
Пусть η η eta\etaη - случайная величина со средним значением m η m η m_(eta)m_{\eta}mη и СКО σ η σ η sigma_(eta)\sigma_{\eta}ση. Неравенство Чебышева
P ( | η − m η | ≤ k σ η ) ≥ 1 − 1 k 2 , P η − m η ≤ k σ η ≥ 1 − 1 k 2 , P(|eta-m_(eta)| <= ksigma_(eta)) >= 1-(1)/(k^(2)),P\left(\left|\eta-m_{\eta}\right| \leq k \sigma_{\eta}\right) \geq 1-\frac{1}{k^{2}},P(|η−mη|≤kση)≥1−1k2,
позволяет определить интервал [ m η − k σ η , m η + k σ η ] m η − k σ η , m η + k σ η [m_(eta)-ksigma_(eta),m_(eta)+ksigma_(eta)]\left[m_{\eta}-k \sigma_{\eta}, m_{\eta}+k \sigma_{\eta}\right][mη−kση,mη+kση], в который с заданной вероятностью p p ppp попадают значения случайной величины η η eta\etaη. В самом деле, пусть p , 0 < p < 1 p , 0 < p < 1 p,0 < p < 1p, 0<p<1p,0<p<1. Приравняв правую часть неравенства Чебышева к p p ppp, получаем уравнение 1 − 1 k 2 = p 1 − 1 k 2 = p 1-(1)/(k^(2))=p1-\frac{1}{k^{2}}=p1−1k2=p относительно k k kkk. Его решением является k = 1 / ( 1 − p ) 1 / 2 k = 1 / ( 1 − p ) 1 / 2 k=1//(1-p)^(1//2)k=1 / (1-p)^{1 / 2}k=1/(1−p)1/2, при котором в указанный выше интервал попадают 100 p % 100 p % 100 p%100 p \%100p% значений случайной величины η η eta\etaη. После замены неизвестных m Q ∖ A m Q ∖ A m_(Q\\A)m_{Q \backslash A}mQ∖A и σ Q ∖ A σ Q ∖ A sigma_(Q\\A)\sigma_{Q \backslash A}σQ∖A их оценками, интервал принимает вид
[ x ¯ Q ∖ A − k s Q ∖ A , x ¯ Q ∖ A + k s Q ∖ A ] . x ¯ Q ∖ A − k s Q ∖ A , x ¯ Q ∖ A + k s Q ∖ A . [ bar(x)_(Q\\A)-ks_(Q\\A), bar(x)_(Q\\A)+ks_(Q\\A)].\left[\bar{x}_{Q \backslash A}-k s_{Q \backslash A}, \bar{x}_{Q \backslash A}+k s_{Q \backslash A}\right] .[x¯Q∖A−ksQ∖A,x¯Q∖A+ksQ∖A].
Для завершения сегментации осталось выбрать достаточно большое значение p p ppp, чтобы в интервале оказались почти все амплитуды фона, и проверить попадание в этот интервал амплитуд ( x z ) z ∈ Q ∖ F r ( Q ) x z z ∈ Q ∖ F r ( Q ) (x_(z))_(z in Q\\Fr(Q))\left(x_{z}\right)_{z \in Q \backslash F r(Q)}(xz)z∈Q∖Fr(Q) всех внутренних пикселей зоны интереса. Если амплитуда x z x z x_(z)x_{z}xz попала в интервал, то пиксель с координатой z z zzz относится к классу Фон. В противном случае, если амплитуда x z x z x_(z)x_{z}xz оказалась вне интервала, принимается решение о недостаточном ее сходстве с амплитудами пикселей фона. Поэтому такой пиксель следует отнести к классу Объект. Напомним, что по определению зоны интереса пиксели ( ξ z ) z ∈ F r ( Q ) ξ z z ∈ F r ( Q ) (xi_(z))_(z in Fr(Q))\left(\xi_{z}\right)_{z \in F r(Q)}(ξz)z∈Fr(Q), образующие ее границу, принадлежат классу Фон.
Амплитуды пикселей являются случайными величинами. Поэтому амплитуда x z x z x_(z)x_{z}xz пикселя из окрестности объекта может оказаться вне указанного интервала. В этом случае пиксель фона с координатой Z Z ZZZ в соответствии с принятым решающим правилом будет ошибочно отнесен к классу Объект. Вероятность такого события равняется ( 1 − p 1 − p 1-p1-p1−p ).
В 2.4 предлагалось считать амплитуду каждого пикселя суммой двух слагаемых: сигнала и шума. Там же показано, что сглаживание исходного изображения с использованием квадратной окрестности с радиусом r ^ r ^ hat(r)\hat{r}r^ уменьшает шум на сглаженном изображении в ( 2 r ^ + 1 ) ( 2 r ^ + 1 ) (2 hat(r)+1)(2 \hat{r}+1)(2r^+1) раз. На рисунках 4.2.3 и 4.2.4 приведены результаты сегментации зоны интереса с рисунка 4.2.1. В первом случае сегментации подверглось исходное изображение (без сглаживания). Во втором случае перед сегментацией изображение было сглажено с радиусом r ^ = 1 r ^ = 1 hat(r)=1\hat{r}=1r^=1.
Результатом сегментации простой зоны интереса должны быть два связных подмножества: проекция A A AAA самого объекта и проекция Q / A Q / A Q//AQ / AQ/A его окрестности (или фона). Однако, из-за шума и присутствия в зоне интереса пикселей с одинаковыми амплитудами, принадлежащими как объекту, так и фону, в ходе
Рисунок 4.2.3 - Сегментация исходного изображения (без сглаживания)
Рисунок 4.2.4 - Сегментация сглаженного изображения ( r = 1 r = 1 r=1r=1r=1 )
сегментации возникают ошибки. Проекция объекта может увеличиться за счет присоединения некоторых пикселей фона, амплитуды которых оказались вне интервала. Также, она может лишиться части собственных пикселей, если их амплитуды попали в интервал. Поэтому результатом сегментации будут, как правило, два множества A ^ A ^ hat(A)\hat{A}A^ и Q ∖ A ^ Q ∖ A ^ Q\\ hat(A)Q \backslash \hat{A}Q∖A^, отличные от фактических A A AAA и Q / A Q / A Q//AQ / AQ/A. При этом одно из них или оба могут состоять из нескольких изолированных связных подмножеств (компонент). Из определения зоны интереса следует, что в ней может находится только один объект и фон. Поэтому необходимо провести дополнительную операцию - коррекцию результата сегментации. Для этого используются дополнительные признаки, к которым относятся площадь, габаритные размеры, форма, связность проекций объектов и другие. В рассмотренном примере коррекция не проводилась.

4.3 Сегментация сложной зоны интереса

Очевидно, что составным или сложным может быть не только объект, но и фон в зоне интереса. В связи с этим зона интереса будет называться составной или сложной, если составным является или объект или фон, а также, если составными являются одновременно они оба. Исходной информацией о зоне интереса ξ Q ξ Q xi_(Q)\xi_{Q}ξQ с объекта ξ A ξ A xi_(A)\xi_{A}ξA служит ее изображение x Q = ( x z ) z ∈ Q x Q = x z z ∈ Q x_(Q)=(x_(z))_(z in Q)x_{Q}=\left(x_{z}\right)_{z \in Q}xQ=(xz)z∈Q. Для каждого значения амплитуды y ∈ Y y ∈ Y y in Yy \in Yy∈Y по изображению x Q x Q x_(Q)x_{Q}xQ можно подсчитать количество n y n y n_(y)n_{y}ny пикселей зоны интереса, амплитуды которых совпадают с этим значением. Оно будет называться повторяемостью значения y y yyy в отличие от его относительной частоты ( n y / | Q | ) y ∈ Y n y / | Q | y ∈ Y (n_(y)//|Q|)_(y in Y)\left(n_{y} /|Q|\right)_{y \in Y}(ny/|Q|)y∈Y. Иногда, когда это не приводит к неопределенности, семейство повторяемостей ( n y ) y ∈ Y n y y ∈ Y (n_(y))_(y in Y)\left(n_{y}\right)_{y \in Y}(ny)y∈Y будет также называется гистограммой изображения.
Для сегментации сложных зон интереса предлагается воспользоваться следующими соображениями. Во-первых, предполагается, что на гистограмме зоны интереса для каждого простого объекта, включая фон, должен присутствовать свой локальный максимум. Каждый локальный максимум соответствует фрагменту однородного случайного поля, описывающего составную часть сложного объекта или составную часть фона. При этом точка максимума является амплитудой, совпадающей со средним значением соответствующего фрагмента однородного случайного поля. В случае сложной зоны интереса их на гистограмме должно быть не менее трех. Во-вторых, также предполагается, что амплитуды пикселей каждого объекта группируются вокруг точки, соответствующей его локальному максимуму. Поэтому для разделения амплитуд, оказавшихся между соседними локальными максимумами (левым и правым) предлагается использовать точку наименьшего локального минимума, находящегося между ними. Пиксели с амплитудами, оказавшимися слева от точки минимума, предлагается считать принадлежащими объекту, которому соответствует левый локальный максимум. Пиксели с амплитудами, оказавшимися справа от точки минимума, предлагается считать принадлежащими объекту, которому соответствует правый локальный минимум. Пиксели, амплитуда которых совпала с амплитудой точки минимума, могут быть отнесены к любому из указанных объектов.
Признаком составной зоны интереса является гистограмма с тремя и более реальными локальными максимумами. По-видимому, наиболее легкой, с точки зрения сегментации, является зона интереса, содержащая простой объект и сложный фон. Пример реального изображения с такой зоной и ее гистограмма представлены на рисунках 4.3.1 и 4.3.2 соответственно. Составляющие зону интереса пиксели образуют прямоугольник с выделенной границей. Визуальный анализ изображения зоны интереса позволяет без труда убедиться в том, что фон объекта состоит из трех фрагментов, амплитуды которых отличаются средними значениями. Этот вывод подтверждается и гисто-
граммой. Следует обратить внимание на ряд отдельных пикселей, находящихся возле левой вертикальной границы зоны, амплитуды которых заметно отличаются от амплитуд своих соседей, что свидетельствует о повреждении соответствующих элементов матрицы ФПУ.
На рисунках 4.3.3 и 4.3.4 приведены изображение с зоной интереса со сложным объектом и простым фоном, а также ее гистограмма. Изображение объекта позволяет уверено утверждать, что он является сложным: состоит из нескольких фрагментов однородных случайных полей с разными средними значениями. Что подтверждается гистограммой.
Рисунок 4.3.3 - Зона интереса со сложным объектом Рисунок 4.3.4 - Гистограмма зоны интереса со сложным объектом
https://cdn.mathpix.com/cropped/eb530be6-5346-4fc5-8ad9-46eb76334cd8-77.jpg?height=314&width=300&top_left_y=1589&top_left_x=497 https://cdn.mathpix.com/cropped/eb530be6-5346-4fc5-8ad9-46eb76334cd8-77.jpg?height=468&width=782&top_left_y=1511&top_left_x=1118 Рисунок 4.3.3 - Зона интереса со сложным объектом Рисунок 4.3.4 - Гистограмма зоны интереса со сложным объектом| 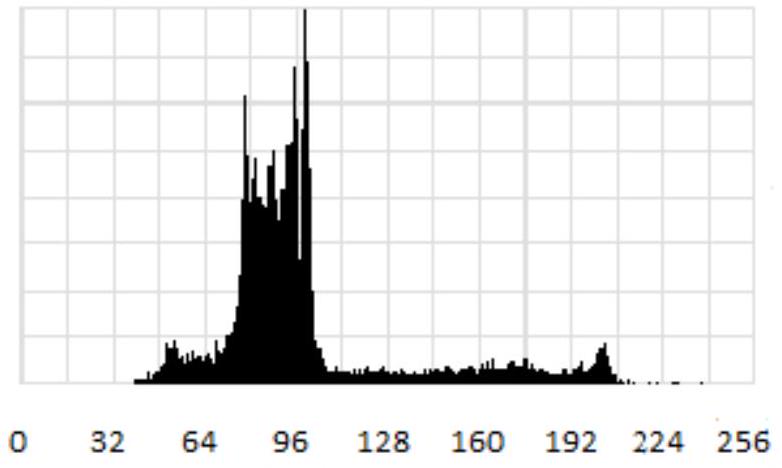![](https://cdn.mathpix.com/cropped/eb530be6-5346-4fc5-8ad9-46eb76334cd8-77.jpg?height=314&width=300&top_left_y=1589&top_left_x=497) | ![](https://cdn.mathpix.com/cropped/eb530be6-5346-4fc5-8ad9-46eb76334cd8-77.jpg?height=468&width=782&top_left_y=1511&top_left_x=1118) | | :--- | :--- | | Рисунок 4.3.3 - Зона интереса со сложным объектом | Рисунок 4.3.4 - Гистограмма зоны интереса со сложным объектом |
Случай, когда сложными являются одновременно объект и фон представлен на рисунках 4.3.5 и 4.3.6. В изображении объекта можно выделить, как минимум, два фрагмента, амплитуды которых отличаются разными средними значениями. Это пиксели лобового стекла и пиксели металлического кузова. Пиксели, образующие фон, делятся на две разные по величине части. Средняя амплитуда оказавшихся в тени пикселей, значительно ниже средней амплитуды пикселей остальной, большой части фона. Однако средняя амплитуда оказавшихся в тени пикселей близка к средней амплитуде кузова. Это обстоятель-
ство усложняет сегментацию. На гистограмме зоны интереса два явны локальных максимума. Что больше соответствует простой зоне интереса.
К сожалению, фактическое количество присутствующих на гистограмме локальных максимумов оказывается, как правило, значительно больше числа объектов в зоне интереса. Это подтверждают приведенные выше гистограммы. Поэтому вначале придется научиться отличать максимумы, вызванные случайными изменениями амплитуд (они будут называться ложными), от максимумов, соответствующих простым объектам из зоны интереса. Эти максимумы будут называться значимыми. Для этого требуется уточнить определение локального максимума гистограммы.
Рисунок 4.3.5 - Зона интереса со сложными объектом и фоном Рисунок 4.3.6 - Гистограмма зоны интереса со сложыми объектом и фоном
https://cdn.mathpix.com/cropped/eb530be6-5346-4fc5-8ad9-46eb76334cd8-78.jpg?height=392&width=396&top_left_y=893&top_left_x=471 https://cdn.mathpix.com/cropped/eb530be6-5346-4fc5-8ad9-46eb76334cd8-78.jpg?height=451&width=785&top_left_y=837&top_left_x=1112 Рисунок 4.3.5 - Зона интереса со сложными объектом и фоном Рисунок 4.3.6 - Гистограмма зоны интереса со сложыми объектом и фоном| 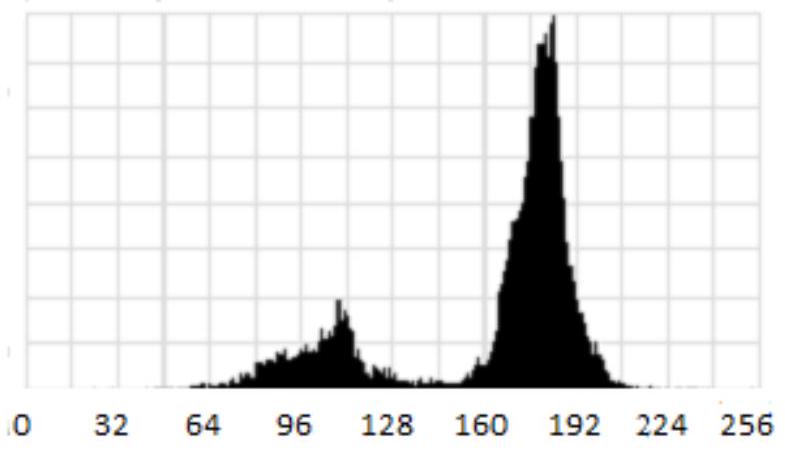![](https://cdn.mathpix.com/cropped/eb530be6-5346-4fc5-8ad9-46eb76334cd8-78.jpg?height=392&width=396&top_left_y=893&top_left_x=471) | ![](https://cdn.mathpix.com/cropped/eb530be6-5346-4fc5-8ad9-46eb76334cd8-78.jpg?height=451&width=785&top_left_y=837&top_left_x=1112) | | :--- | :--- | | Рисунок 4.3.5 - Зона интереса со сложными объектом и фоном | Рисунок 4.3.6 - Гистограмма зоны интереса со сложыми объектом и фоном |
Будем называть амплитуду j ∈ Y j ∈ Y j in Yj \in Yj∈Y точкой локального максимума, а соответствующую ей повторяемость n j n j n_(j)n_{j}nj локальным максимумом, если выполняются следующие два условия. Во-первых, слева и справа от j j jjj присутствуют амплитуды i i iii с повторяемостью n i n i n_(i)n_{i}ni и амплитуда l l lll с повторяемость n l n l n_(l)n_{l}nl такие, что n i < n j n i < n j n_(i) < n_(j)n_{i}<n_{j}ni<nj и n l < n j n l < n j n_(l) < n_(j)n_{l}<n_{j}nl<nj. Во-вторых, для всех амплитуд k , i < k < j k , i < k < j k,i < k < jk, i<k<jk,i<k<j, и всех амплитуд s , j < s < l s , j < s < l s,j < s < ls, j<s<ls,j<s<l, (если такие найдутся) выполняется равенство n k = n j = n l n k = n j = n l n_(k)=n_(j)=n_(l)n_{k}=n_{j}=n_{l}nk=nj=nl. Пусть x min x min x_(min)x_{\min }xmin и x max x max x_(max)x_{\max }xmax - минимальная и максимальная амплитуды на изображении x Q x Q x_(Q)x_{Q}xQ. Будем называть амплитуду x min x min x_(min)x_{\min }xmin также точкой локального максимума, если, вопервых, справа от нее присутствует амплитуда l l lll такая, что n l < n x min n l < n x min n_(l) < n_(x_(min))n_{l}<n_{x_{\min }}nl<nxmin. Во-вторых, для всех s , x min < s < l s , x min  < s < l s,x_("min ") < s < ls, x_{\text {min }}<s<ls,xmin <s<l, выполняется n x min = n s n x min  = n s n_(x_("min "))=n_(s)n_{x_{\text {min }}}=n_{s}nxmin =ns. По этой же причине будем называть x max x max x_(max)x_{\max }xmax точкой локального максимума, если слева от нее найдется амплитуда i i iii с повторяемостью n i n i n_(i)n_{i}ni такая, что n i < n x max n i < n x max n_(i) < n_(x_(max))n_{i}<n_{x_{\max }}ni<nxmax и если для всех k k kkk, i < k < n x max i < k < n x max i < k < n_(x_(max))i<k<n_{x_{\max }}i<k<nxmax, выполняется n x max = n k n x max = n k n_(x_(max))=n_(k)n_{x_{\max }}=n_{k}nxmax=nk.
Разделение локальных максимумов на ложные и значимые предлагается выполнять с помощью методов математической статистики. Вначале для каждого локального максимума требуется определить ближайшие к нему левую x L x L x_(L)x_{L}xL и правую x R x R x_(R)x_{R}xR точки локальных минимумов. Затем следует выбрать уровень значимсти α α alpha\alphaα и проверить гипотезу о том, что распределение амплитуд на ин-
тервале [ x L , x R ] x L , x R [x_(L),x_(R)]\left[x_{L}, x_{R}\right][xL,xR] является равномерным. В случае принятия гипотезы локальный максимум на интервале [ x L , x R ] x L , x R [x_(L),x_(R)]\left[x_{L}, x_{R}\right][xL,xR] считается ложным. В противном случае - значимым на уровне α α alpha\alphaα. Проверка этой гипотезы подробно изложена в п. 1.8.
При проверке гипотезы требуется соблюдать следующие условия [xx]. Во-первых, для повторяемости n j n j n_(j)n_{j}nj каждой амплитуды x L ≤ j ≤ x R x L ≤ j ≤ x R x_(L) <= j <= x_(R)x_{L} \leq j \leq x_{R}xL≤j≤xR должно выполняться неравенство n j ≥ n min n j ≥ n min n_(j) >= n_(min)n_{j} \geq n_{\min }nj≥nmin. В случае использования критерия χ 2 n min = 5 χ 2 n min  = 5 chi^(2)n_("min ")=5\chi^{2} n_{\text {min }}=5χ2nmin =5. Во-вторых, сумма повторяемостей n j n j n_(j)n_{j}nj амплитуд, x L ≤ j ≤ x R x L ≤ j ≤ x R x_(L) <= j <= x_(R)x_{L} \leq j \leq x_{R}xL≤j≤xR, не должна быть меньше 50.

Если для исходной гистограммы указанные условия не выполняются, то ее можно изменить

Пусть n y n y n_(y)n_{y}ny - количество пикселей зоны интереса со значением y ∈ Y y ∈ Y y in Yy \in Yy∈Y, называемое повторяемостью этого значения, а
a = min 1 ≤ j ≤ n ( x j ) , b = max 1 ≤ j ≤ n ( x j ) a = min 1 ≤ j ≤ n   x j , b = max 1 ≤ j ≤ n   x j a=min_(1 <= j <= n)(x_(j)),b=max_(1 <= j <= n)(x_(j))a=\min _{1 \leq j \leq n}\left(x_{j}\right), b=\max _{1 \leq j \leq n}\left(x_{j}\right)a=min1≤j≤n(xj),b=max1≤j≤n(xj)
  • минимальное и максимальное значения амплитуд в зоне интереса. Разделим интервал [ a , b ] [ a , b ] [a,b][a, b][a,b] точками ( a j ) 1 ≤ j ≤ N + 1 a j 1 ≤ j ≤ N + 1 (a_(j))_(1 <= j <= N+1)\left(a_{j}\right)_{1 \leq j \leq N+1}(aj)1≤j≤N+1,
a = a 1 < ⋯ < a N + 1 = b a = a 1 < ⋯ < a N + 1 = b a=a_(1) < cdots < a_(N+1)=ba=a_{1}<\cdots<a_{N+1}=ba=a1<⋯<aN+1=b
на N N NNN непересекающихся подинтервалов [ a j , a j + 1 [ , 1 ≤ j < N a j , a j + 1 , 1 ≤ j < N [a_(j),a_(j+1)[,1 <= j < N:}\left[a_{j}, a_{j+1}\left[, 1 \leq j<N\right.\right.[aj,aj+1[,1≤j<N, и [ a N , a N + 1 ] a N , a N + 1 [a_(N),a_(N+1)]\left[a_{N}, a_{N+1}\right][aN,aN+1] таким образом, чтобы количество n j n j n_(j)n_{j}nj амплитуд, оказавшихся в каждом подинтервал [ a j , a j + 1 [ a j , a j + 1 [a_(j),a_(j+1)[:}\left[a_{j}, a_{j+1}\left[\right.\right.[aj,aj+1[, составляло не менее n min n min  n_("min ")n_{\text {min }}nmin  значений. Величина n min n min  n_("min ")n_{\text {min }}nmin  зависит от проверяемой гипотезы и применяемого критерия значимости. В рассматриваемом случае должно выполняться неравенство n min ≥ 5 n min  ≥ 5 n_("min ") >= 5n_{\text {min }} \geq 5nmin ≥5. Назовем точкой локального максимума подинтервал [ a j , a j + 1 [ a j , a j + 1 [a_(j),a_(j+1)[:}\left[a_{j}, a_{j+1}\left[\right.\right.[aj,aj+1[, содержащий n j n j n_(j)n_{j}nj значений, для которого выполняются следующие два условия. Во-первых, слева от него существует подинтервал [ a i , a i + 1 [ a i , a i + 1 [a_(i),a_(i+1)[:}\left[a_{i}, a_{i+1}\left[\right.\right.[ai,ai+1[ такой, что n i < n j n i < n j n_(i) < n_(j)n_{i}<n_{j}ni<nj. При этом для всех подинтервалов [ a k , a k + 1 [ a k , a k + 1 [a_(k),a_(k+1)[:}\left[a_{k}, a_{k+1}\left[\right.\right.[ak,ak+1[ с номерами i < k < j i < k < j i < k < ji<k<ji<k<j выполняется равенство n k = n j n k = n j n_(k)=n_(j)n_{k}=n_{j}nk=nj. Во-вторых, справа от [ a j , a j + 1 [ a j , a j + 1 [a_(j),a_(j+1)[:}\left[a_{j}, a_{j+1}\left[\right.\right.[aj,aj+1[ существует подинтервал [ a l , a l + 1 [ a l , a l + 1 [a_(l),a_(l+1)[:}\left[a_{l}, a_{l+1}\left[\right.\right.[al,al+1[ такой, что n l < n j n l < n j n_(l) < n_(j)n_{l}<n_{j}nl<nj. Для всех подинтервалов [ a s , a s + 1 [ a s , a s + 1 [ [a_(s),a_(s+1)[:}\left[a_{s}, a_{s+1}[\right.[as,as+1[ с номерами j < s < l j < s < l j < s < lj<s<lj<s<l выполняется равенство n s = n j n s = n j n_(s)=n_(j)n_{s}=n_{j}ns=nj. Подинтервал [ a j , a j + 1 [ a j , a j + 1 [ [a_(j),a_(j+1)[:}\left[a_{j}, a_{j+1}[\right.[aj,aj+1[ будет называться локальным максимумом на уровне значимости α α alpha\alphaα, если на этом уровне отклоняется гипотеза о равномерном распределении амплитуд на интервале [ a i , a l + 1 [ a i , a l + 1 [ [a_(i),a_(l+1)[:}\left[a_{i}, a_{l+1}[\right.[ai,al+1[.
*/

4.4 Отбраковка зон интереса
0
32
64
96
128
160
192
124
256
0 32 64 96 128 160 192 124 256| 0 | | :--- | | 32 | | 64 | | 96 | | 128 | | 160 | | 192 | | 124 | | 256 |
https://cdn.mathpix.com/cropped/eb530be6-5346-4fc5-8ad9-46eb76334cd8-80.jpg?height=580&width=558&top_left_y=449&top_left_x=421 "0 32 64 96 128 160 192 124 256" | ![](https://cdn.mathpix.com/cropped/eb530be6-5346-4fc5-8ad9-46eb76334cd8-80.jpg?height=580&width=558&top_left_y=449&top_left_x=421) | 0 <br> 32 <br> 64 <br> 96 <br> 128 <br> 160 <br> 192 <br> 124 <br> 256 | | :--- | :--- | | | |
Навигация